Cách nhận dạng đồ thị hàm số bậc 4 trùng phương cực hay - Toán lớp 12

---

Cách nhận dạng đồ thị hàm số bậc 4 trùng phương cực hay

Với Cách nhận dạng đồ thị hàm số bậc 4 trùng phương cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập nhận dạng đồ thị hàm số bậc 4 trùng phương từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax⁴ + bx² + c     (a ≠ 0)

   Đồ thị có 3 điểm cực trị :

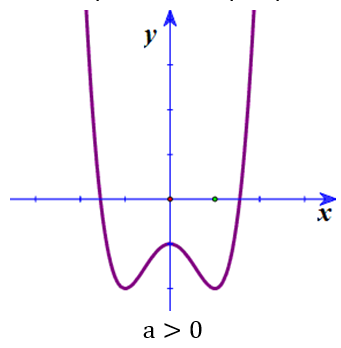
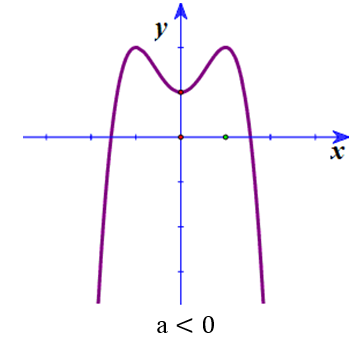
   Đồ thị có 1 điểm cực trị :

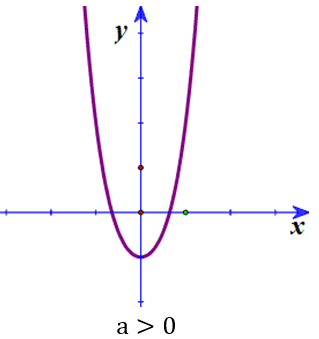
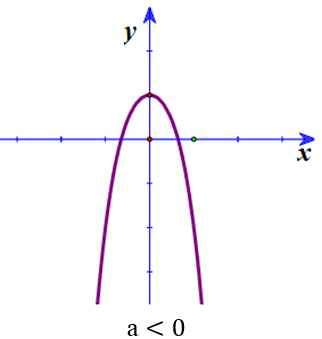
   Đồ thị hàm bậc bốn trùng phương luôn nhận trục tung làm trục đối xứng

Ví dụ minh họa

Ví dụ 1: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

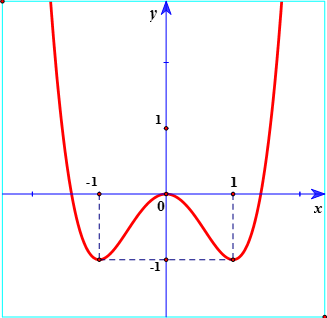
   A. y = x⁴ - 3x²+1.     B. y = x⁴ + 2x².

   C. y = x⁴ - 2x².     D. y = -x⁴ - 2x².

Hướng dẫn

Từ đồ thị và đáp án suy ra đây là hàm số bậc 4 trùng phương: y = ax⁴ + bx² + c     (a ≠ 0) có 3 cực trị nên a > 0,b < 0. Do đó loại B, D. Do đồ thị qua O(0; 0)nên c = 0 loại A.

Từ đồ thị suy ra hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = ±1 nên loại A, B, D.

Chọn C.

Ví dụ 2: Giả sử hàm số y = ax⁴ + bx² + c có đồ thị là hình bên dưới. Tìm a,b, c.

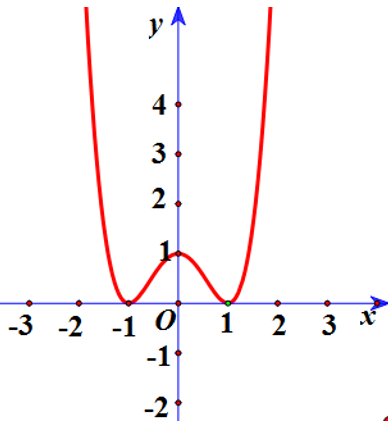
Hướng dẫn

y' = 4ax³ + 2bx

Nhìn đồ thị ta thấy :

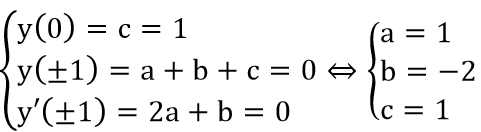
Ví dụ 3: Cho hàm số y=f(x) có đồ thị (C) như hình vẽ. Chọn khẳng định sai về hàm số f(x):

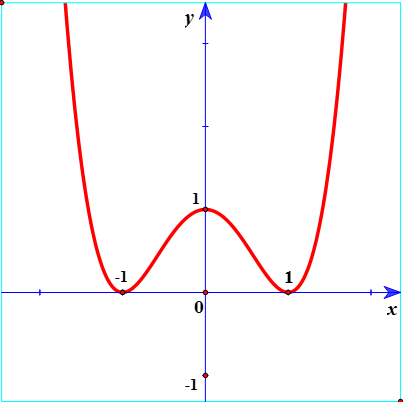
   A. Hàm số f(x) tiếp xúc với Ox.

   B. Hàm số f(x) đồng biến trên (-1; 0).

   C. Hàm số f(x) nghịch biến trên (-∞; -1).

   D. Đồ thị hàm số f(x) có tiệm cận ngang là y = 0.

Hướng dẫn

Từ đồ thị ta suy ra các tính chất của hàm số:

   1. Hàm số đạt CĐ tại x = 0 và đạt CT tại x = ±1.

   2. Hàm số tăng trên (-1; 0) và (1; +∞).

   3. Hàm số giảm trên (-∞; -1) và (0; 1).

   4. Hàm số không có tiệm cận.

Chọn D.

B. Bài tập vận dụng

Bài tập nhận dạng đồ thị hàm số bậc 4 trùng phương

Câu 1:

   A. y = -x⁴ + 4x² - 3     B. y = -x⁴ + 4x² - 4

   C. y = x⁴ - 4x² + 1     D. y = x⁴ + 4x² + 1

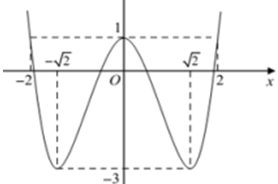
Lời giải:

Đáp án : C

Câu 2:

   A. y = x⁴ +x² + 2     B. y = x⁴ + x² + 1

   C. y = x⁴ -x² + 2     D. y = x⁴ - x² + 1

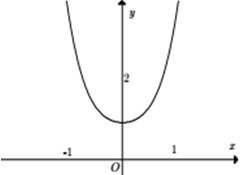
Lời giải:

Đáp án : B

Câu 3:

   A. y=-2x⁴ + 4x² - 1     B. y = x⁴ - 2x² - 1

   C. y=-x⁴ +2x² - 1     D. y = -x⁴ + 2x² + 1

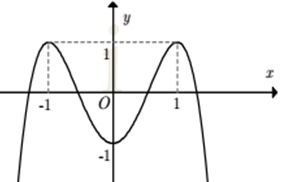
Lời giải:

Đáp án : A

Câu 4:

   A. y = x⁴ +2x² +3     B. y = -x⁴ - 2x² + 3

   C. y=-x⁴ +2x² +3     D. y = -x⁴ - 2x² - 3

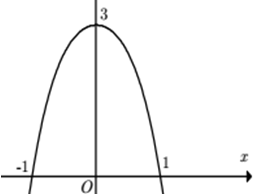
Lời giải:

Đáp án : B

Câu 5:

   A. y = x⁴ -2x² -2     B. y = -x⁴ + 2x²

   C. y = x⁴ -2x²     D. y = x⁴ - 2x² - 1

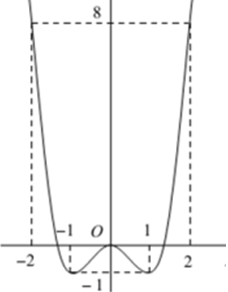
Lời giải:

Đáp án : C

Câu 6:

   A. y = x⁴ +x² +6     B. y = -x⁴ - x²

   C. y = x⁴ -5x² +6     D. y = -x⁴ - x² + 6

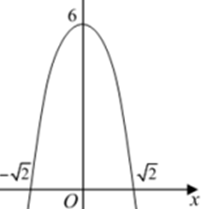
Lời giải:

Đáp án : D

Câu 7:

   A. y = x⁴ - 2x² +2     B. y = x⁴ - 2x² + 3

   C. y = x⁴ - 4x² +2     D. y = -x⁴ + 2x² + 2

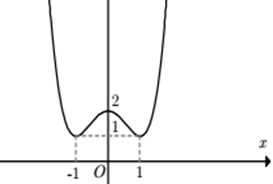
Lời giải:

Đáp án : A

Câu 8:

   A. y = 1/2 x⁴ - x² +3     B. y = -1/4 x⁴ + 2x² + 3

   C. y = 1/2 x⁴ - 2x² -1     D. y = 1/4 x⁴ - 2x² + 3

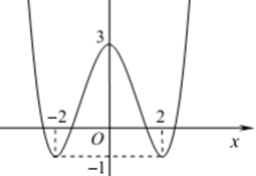
Lời giải:

Đáp án : D

Câu 9:

   A. y = x⁴ - 2x²     B. y = (-1/4)x⁴ + 2x²

   C. y = 1/4 x⁴ - 4x²     D. y = -1/2 x⁴ + x²

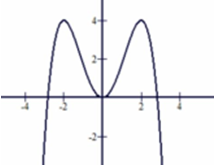
Lời giải:

Đáp án : B

Câu 10:

   A. y = -3x⁴ - 4x² + 2     B. y = -x⁴ + 2x² + 2

   C. y = -1/2 x⁴ - x² + 2     D. y = -x⁴ + 3x² + 2

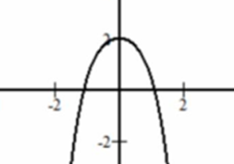
Lời giải:

Đáp án : C

Câu 11: Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình bên. Chọn khẳng định đúng:

   A. a > 0,b > 0,c > 0     B. a < 0,b > 0,c < 0

   C. a < 0,b > 0,c > 0     D. a < 0,b < 0,c < 0

Lời giải:

Đáp án : C

Câu 12: Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình bên. Chọn khẳng định đúng:

   A. a > 0,b > 0     B. a > 0,b < 0

   C. a < 0,b > 0     D. a < 0,b < 0

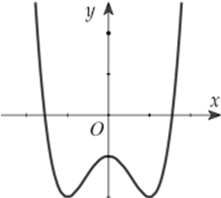
Lời giải:

Đáp án : B

Câu 13: Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình bên. Chọn khẳng định đúng:

   A. a > 0,b < 0,c < 0     B. a < 0,b > 0,c > 0

   C. a > 0,b > 0,c > 0     D. a > 0,b < 0,c > 0

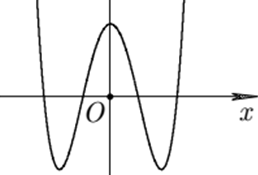
Lời giải:

Đáp án : D

Câu 14: Cho hàm số y = ax⁴ + bx² + c (a ≠ 0), có đồ thị như hình bên. Chọn khẳng định đúng:

   A. a < ,b ≤ 0,c > 0     B. a < 0,b < 0,c < 0

   C. a > 0,b > 0,c > 0     D. a < 0,b > 0,c ≥ 0

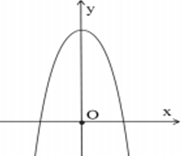
Lời giải:

Đáp án : A