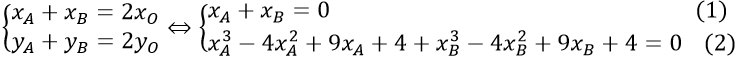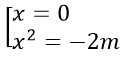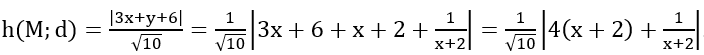Bài tập trắc nghiệm Điểm đặc biệt thuộc đồ thị hàm số cực hay (điểm cố định, điểm đối xứng, ...) - Toán lớp 12

---

Bài tập trắc nghiệm Điểm đặc biệt thuộc đồ thị hàm số cực hay (điểm cố định, điểm đối xứng, ...)

Với Bài tập trắc nghiệm Điểm đặc biệt thuộc đồ thị hàm số cực hay (điểm cố định, điểm đối xứng, ...) Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Điểm đặc biệt thuộc đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Đồ thị của hàm số y = x² + 2mx - m + 1 (m là tham số) luôn đi qua một điểm Mcố định có tọa độ là

A. M(0; 1).    B. M(1/2; 3/2).    C. M(1/2; 5/4).    D. M(-1; 0).

Lời giải:

Đáp án : C

Giải thích :

Gọi M(x_o;y_o) là điểm cố định cần tìm.

Ta có y_o = x_o² + 2mx_o - m + 1

⇔ (2x_o- 1)m + x_o² + 1 - y_o = 0,∀m⇔ 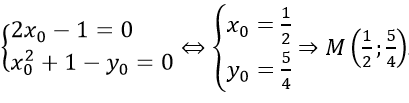⇒ M(1/2; 5/4).

Bài 2: Biết đồ thị (C_m) của hàm số y = x⁴ - 2mx² + 3 luôn đi qua một điểm M cố định khi m thay đổi, khi đó tọa độ của điểm M là

A. M(-1; 1).    B. M(1; 4).    C. M(0; -2).    D. M(0; 3).

Lời giải:

Đáp án : D

Giải thích :

Gọi M(x_o; y_o) là điểm cố định cần tìm.

Ta có

y_o=x_o⁴ -2mx_o² + 3,∀m⇔ 2x_o² m + y_o - 3 - x_o⁴ = 0,∀m⇔ 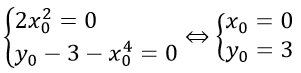⇒ M(0;3).

Bài 3: Biết đồ thị (C_m) của hàm số y=[(m+1)x + m]/(x + m) (m ≠ 0) luôn đi qua một điểm M cố định khi m thay đổi. Tọa độ điểm M khi đó là

A. M(-1; -1/2).    B. M(0; 1).    C. M(-1; 1).    D. M(0; -1).

Lời giải:

Đáp án : B

Giải thích :

Gọi M(x_o;y_o) là điểm cố định cần tìm.

Ta có y_o=((m + 1)x_o + m)/(x_o+ m) ,∀m≠0⇔ x_o y_o+my_o = mx_o + x_o + m ,∀m ≠ 0

⇔ m(y_o - x_o-1) + x_o y_o - x_o = 0,∀m ≠ 0⇔ 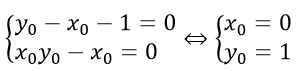⇒ M(0; 1).

Bài 4: Trên đồ thị (C) của hàm số y = 3/(2x - 1) có bao nhiêu điểm có tọa độ là các số nguyên dương

A. 4.    B. 3.    C. 1.    D. 2.

Lời giải:

Đáp án : D

Giải thích :

Gọi M(x_o;y_o) với x_o ∈ N*,y_o ∈ N*

⇒ ⇒ 2x_o - 1 ∈ {1; 3} ⇒ x_o ∈ {1; 2}

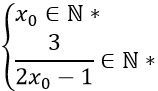
⇒ M₁(-1; -1),M₂(0; -3),M₃(1; 3) và M₄(2; 1).

   Vậy trên đồ thị (C) có hai điểm có tọa độ là các số nguyên dương

Bài 5: Trên đồ thị (C) của hàm số y = (x + 2)/(2x - 1) có bao nhiêu điểm có tọa độ nguyên

A. 4.    B. 2.    C. 1.    D. 6.

Lời giải:

Đáp án : A

Giải thích :

Gọi M(x_o; y_o) với x_o ∈ Z, y_o ∈ Z.

⇒ ⇒ 2x_o-1∈{-5;-1;1;5} ⇒ x_o∈{-2;0;1;3}

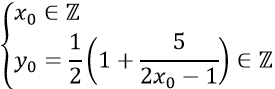
⇔ x_o=-2 ⇒ y_o=0 ⇒ M(-2;0) ⇔ x_o= 1 ⇒ y_o=3 ⇒ M(1;3)

⇔ x_o=0 ⇒ y_o=-2 ⇒ M(0;-2) ⇔ x_o= 3 ⇒ y_o=1 ⇒ M(3;1)

   Vậy trên đồ thị (C) có bốn điểm có tọa độ là các số nguyên.

Bài 6: Cặp điểm thuộc đồ thị (C) của hàm số y = x³ - 4x² + 9x + 4 đối xứng nhau qua gốc tọa độ O là?

A. (3; 22) và (-3; -22).    B. (2; 14) và (-2; -14).

C. (1; 10) và (-1; -10).    D. (0; 4) và (4; 40).

Lời giải:

Đáp án : C

Giải thích :

Gọi A(x_A;x_A³ - 4x_A² + 9x_A + 4), B(x_B; x_B³ - 4x_B² + 9x_B + 4) là hai điểm trên (C) đối xứng nhau qua gốc tọa độ.

Ta có

Thay (1) vào (2) ta được

x_A³ -4x_A² + 9x_A + 4 + (-x_A )³ - 4(-x_A )² + 9(-x_A) + 4 = 0⇔ .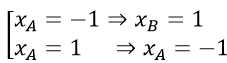

   Vậy cặp điểm cần tìm là A(1; 10), B(-1; -10).

Bài 7: Cặp điểm thuộc đồ thị (C) của hàm số y = x³ + x đối xứng nhau qua đường thẳng d: y = -1/2 x là:

A. (1; 2) và (-2; -10).    B. (2; -1) và (-2; 1).

C. (1; -2) và (-1; 2).    D. (1; 2) và (-1; -2).

Lời giải:

Đáp án : D

Giải thích :

Gọi A(a;a³ +a),B(b;b³ +b) là hai điểm trên (C) đối xứng nhau qua đường thẳng d: y = -1/2 x hay d:x+2y=0.

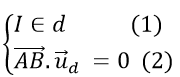
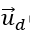
Ta có: (với I là trung điểm của AB và (2;-1) là vecto chỉ phương của d)

Từ (1) ta có (a³ + a + b³ + b)/2 = -1/2.(a + b)/2

⇔ (a + b)(2a² - 2ab + 2b² + 3) = 0⇔ a = -b (3)

(vì 2a² - 2ab + 2b² + 3 = 2(a² - ab + b² + 3/2) = 2(a - 1/2 b)² + 3/2 b² +3>0,∀a,b)

Với (AB)=(b - a; (b - a)(a² + ab + b² +2)), từ (2) ta có

2(b - a) - (b - a)(a² + ab + b² + 1) = 0

⇔ (b - a)(a² + ab + b² - 1) = 0

⇒ a² + ab + b² - 1 = 0 (4) (Vì a≠ b)

Thay (3) vào (4) ta được a² - a² +a² -1=0 ⇔ .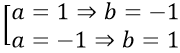

   Vậy cặp điểm cần tìm là A(1; 2), B(-1; -2).

Bài 8: Cho điểm M thuộc đồ thị (C) của hàm số y = (x - 7)/(x + 1), biết M có hoàng độ a và khoảng cách từ Mđến trục Ox bằng ba lần khoảng cách từ Mđến trục Oy. Giá trị có thể có của a là

A. a = 1 hoặc a = 7/3.    B. a = -1 hoặc x = 7/3.

C. a = -1 hoặc a = -7/3.    D. a = 1 hoặc a = -7/3.

Lời giải:

Đáp án : D

Giải thích :

Gọi M(a;(a - 7)/(a + 1)) với a ≠ -1. Theo đề ta có: |(a - 7)/(a + 1)| = 3|a|⇔ .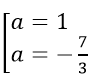

Bài 9: Tập hợp tất cả các giá trị thực của m để trên đồ thị (C_m) của hàm số y = (x² - 4mx + 5m)/(x - 2) có hai điểm phân biệt đối xứng nhau qua gốc tọa độ là

A. (0; +∞).    B. (-1/2; 0)\{-4/13}.

C. [1; +∞).    D. (-∞; 0)∪(1/2; 4/3)∪(4/3; +∞).

Lời giải:

Đáp án : D

Giải thích :

Đồ thị hàm số (Ca_m) có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi và chỉ khi tồn tại x_o ≠ 2 và x_o ≠ 0 sao cho y(x_o) = -y(-x_o)

⇔ tồn tại x_o ≠ 2 và x_o ≠ 0 sao cho (x_o² - 4mx_o + 5m)/(x_o - 2) = -((-x_o )² - 4m(-x_o) + 5m)/((-x_o) - 2)

⇔ tồn tại x_o ≠ 2 và x_o ≠ 0 sao cho (1 - 2m)x_o² + 5m = 0

⇔ .

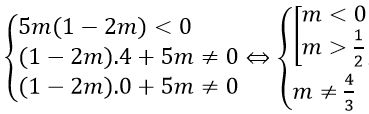
Bài 10: Khoảng cách ngắn nhất từ điểm M thuộc đồ thị (C) của hàm số y = (x² + 2x - 2)/(x - 1) đến I(1, 4) là

A. 2.    B. 2√2.    C. √(2 + 2√2) .    D. √(2√2 - 2).

Lời giải:

Đáp án : C

Giải thích :

Gọi M(x; y) thuộc (C), ta có

.

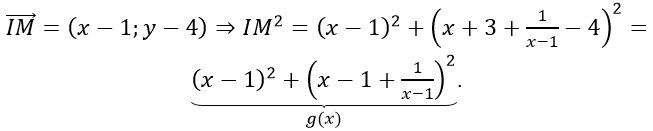
Mà g(x) = (x - 1)² + (x - 1)² + 1/(x - 1)² + 2 = 2(x - 1)² + 1/(x - 1)² + 2 ≥ 2 + 2√2.

⇒ minIM = √(2 + 2√2) . Đạt được khi 2(x-1)² = 1/(x - 1)² ⇔ (x - 1)⁴ = 1/2 ⇒ .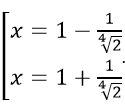

Bài 11: Cho hàm số y =(x + 2)/(x - 3) có đồ thị (C). Tổng khoảng cách từ một điểm M thuộc (C) đến hai hai trục tọa độ đạt giá trị nhỏ nhất bằng ?

A. 2.    B. 2/3.    C. 1.    D. 1/6.

Lời giải:

Đáp án : B

Giải thích :

Điểm M nằm trên trục Ox : M(-2; 0) ⇒ d_M = |-2| + 0 = 2

Điểm M nằm trên trục tung : d_M = 0 + |-2/3| = 2/3 < 2

Xét những điểm M có hoành độ |x|>2/3 ⇒ d_M = |x| + |y| > 2/3.

Xét những điểm M có hoành độ thỏa mãn |x| < 2/3; y < -2/3 ⇒ |y| > 2/3(*)

    Trường hợp : 0 ≤ x ≤ 2/3. Do (*) cho nên : d_M = |x| + |y| > 2/3

    Trường hợp : -2/3 < x < 0;-2/3 < y < 0 ⇒ d_M = -x - 1 - 5/(x - 3); d'_M = -1 + 5/(x - 3)²

d'_M=0⇔ 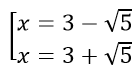. Khi lập bảng biến thiên ,ta thấy hàm số nghịch biến với mọi x∈(-2/3;0). Vậy mind_M=d_M (0)=2/3.

Bài 12: Tọa độ điểm M có hoành độ nguyên thuộc đồ thị (C) của hàm số y = (x + 2)/(x - 1) có khoảng cách đến đường thẳng Δ: x - y + 1 = 0 bằng 1/√2 là

A. M(-2; 0).     B. M(2; 4).

C. M(2; 4);M(-2; 0).    D. M(2; -2).

Lời giải:

Đáp án : C

Giải thích :

Gọi M(a;(a + 2)/(a - 1)) ∈ (C) với a ≠ 1 ta có

|a - (a + 2)/(a - 1) + 1|/√2 = 1/√2⇔ |a² - a - 3|/|a - 1| = 1⇔ .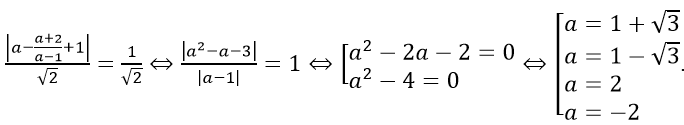

Vậy có hai điểm thỏa yêu cầu là M(2; 4);M(-2; 0).

Bài 13: Cho hàm số y=(x² + 3x + 3)/(x + 2) có đồ thị (C). Tổng khoảng cách từ một điểm M thuộc (C) đến hai hai trục tọa độ đạt giá trị nhỏ nhất bằng ?

A. 1.    B. 1/2.    C. 2.    D. 3/2.

Lời giải:

Đáp án : D

Giải thích :

Điểm M(0,3/2) nằm trên trục Oy. Khoảng cách từ M đến hai trục là d = 3/2.

Xét những điểm M có hoành độ lớn hơn 3/2 ⇒ d = |x| + |y| > 3/2.

Xét những điểm M có hoành độ nhỏ hơn 3/2:

    Với 0 < x < 3/2 ⇒ y > 3/2 ⇒ d = |x| + |y| > 3/2

    Với -3/2 < x < 0; y > 0 ⇒ d = -x + x + 1 + 1/(x + 2) = 1 + 1/(x + 2); d' = -1/(x + 2)² < 0.

   Chứng tỏ hàm số nghịch biến. Suy ra min d=y(0)=3/2.

Bài 14: Điều kiện của tham số m để trên đồ thị (C_m) của hàm số y = x³ -(3m - 1)x² + 2mx + m + 1 có ít nhất hai điểm phân biệt đối xứng nhau qua trục Oy là

A. m ≤ 0.    B. m < 0.    C. m = -2.    D. m ≤ -2.

Lời giải:

Đáp án : B

Giải thích :

Gọi M(x, y),N(-x, y) là hai điểm thuộc đồ thị (C_m)đối xứng nhau qua trục tung. Ta có

   Vậy m < 0.

Bài 15: Khoảng cách nhỏ nhất từ một điểm thuộc đồ thị (C) của hàm số y = (x² + 4x + 5)/(x + 2) đến đường thẳng d: y + 3x + 6 = 0 bằng

A. 2.    B. 4.    C. √10.    D. 4/√10.

Lời giải:

Đáp án : D

Giải thích :

Gọi M(x, x + 2 + 1/(x + 2)) ∈ (C).

Khoảng cách từ M đến d là h(M; d) cho bởi

Khi x + 2 > 0:

Ta có 4(x + 2) + 1/(x + 2) ≥ 4 dấu bằng xảy ra khi 4(x + 2) = 1/(x + 2)⇔ (x + 2)² = 1/4 ⇒ x = -3/2

   Vậy h(M; d) đạt giá trị nhỏ nhất là 4/√10.

Khi x + 2 < 0

Ta có -4(x + 2) - 1/((x + 2)) ≥ 4

Dấu bằng xảy ra ⇔ - 4(x + 2) = -1/(x + 2)⇔ (x + 2)² = 1/4 ⇒ x = -5/2.

   Vậy h(M; d) đạt giá trị nhỏ nhất là 4/√10.