Cách tính diện tích hình trụ, thể tích khối trụ cực hay - Toán lớp 12

Cách tính diện tích hình trụ, thể tích khối trụ cực hay

Với Cách tính diện tích hình trụ, thể tích khối trụ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính diện tích hình trụ, thể tích khối trụ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

• Diện tích xung quanh của hình trụ là:
S_xq = 2πrh

• Diện tích toàn phần của hình trụ là:
S_tp = S_xq + S_2day = 2πrh + 2πr²

• Thể tích của khối trụ là: V = S_day.h = 2πr²h

Trong đó, r là bán kính đường tròn đáy của hình trụ.

2. Ví dụ minh họa

Ví dụ 1 Cho hình chữ nhật ABCD có AB = a và góc = 30⁰ . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:

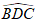
A. √3πa²    B. 2√3πa²    C. 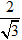πa²    D. πa²

Hướng dẫn giải:

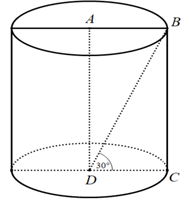
+ Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ.

Hình trụ tạo thành có:

+ Bán kính đường tròn đáy là r = AB = a

+ Đường cao của hình trụ là:
h = BC = CD.tan30⁰ =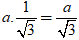

Suy ra, diện tích xung quanh của hình trụ tạo thành là:

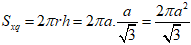
Chọn C.

Ví dụ 2 Một hình tứ diện đều ABCD cạnh a. Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác ABC và có chiều cao bằng chiều cao hình tứ diện. Diện tích xung quanh của hình trụ đó bằng:

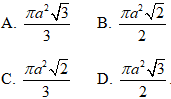
Hướng dẫn giải:

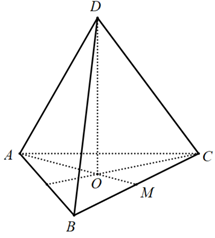
+ Gọi O là tâm của tam giác ABC và M là trung điểm BC. ( khi đó, O là trọng tâm, trực tâm, tâm đường tròn nội tiếp ( ngoại tiếp ) tam giác ABC – vì tam giác ABC đều)

+ Ta có: AM = AM.sinC = a.sin60⁰ =

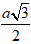
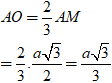
+ Chiều cao tứ diện

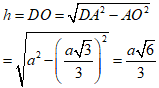
Bán kính đường tròn nội tiếp đáy ABC:
r = OM =

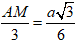
Do đó, diện tích xung quanh của hình trụ tạo thành là:

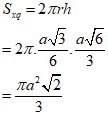
Chọn C.

Ví dụ 3 Cho hình trụ có hai đáy là hình tròn (O) và (O’). Trên hai đường tròn lấy hai điểm A, B sao cho góc giữa AB và mặt phẳng chứa đường tròn đáy bằng 45⁰ và khoảng cách đến trục OO’ bằng . Biết bán kính đáy bằng a, tính thể tích của khối trụ theo a.

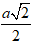
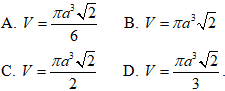
Hướng dẫn giải:

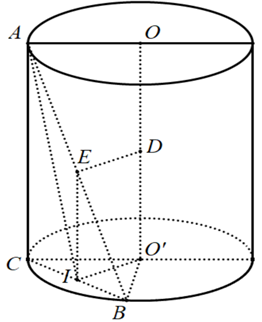
Đặt OO’ = h. Gọi I, E, D lần lượt là trung điểm của BC, BA, OO’.

Ta có: d(AB,OO') = ED = IO' =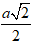

Tam giác ABC vuông tại C có B = 45⁰
⇒ tam giác ABC vuông cân

⇒ BC = AC = h

Ta có: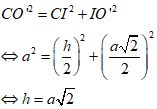

Thể tích khối trụ là: V = πa².a √2 = πa³√2

Chọn B.

Ví dụ 4 Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O; R) và ( O’: R’). Tồn tại dây cung AB thuộc đường tròn (O) sao cho tam giác O’AB là tam giác đều và mặt phẳng (O’AB) hợp với mặt phẳng chứa đường tròn (O) một góc 60⁰. Khi đó, diện tích xung quanh Sxq hình trụ và thể tích V của khối trụ tương ứng là:

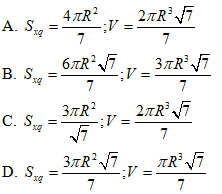
Hướng dẫn giải:

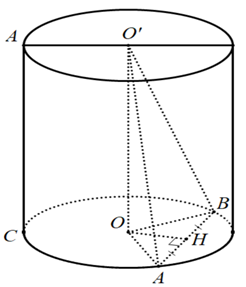
+ Ta có OO’ là trục của hình trụ nên
OO' ⊥ (OAB) .

Gọi H là trung điểm của AB thì

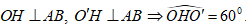
Giả sử OH = x.
Khi đó: 0 < x < R và OO' = x.tan60⁰ = x√3 .

+ Xét tam giác OAH, ta có: AH² = R² – x².

+ Vì tam giác O’AB đều nên:
O'A = AB = 2AH = 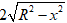(1)

Mặt khác, tam giác AOO’ vuông tại O nên:

AO’² = OO’² + R² = 3x² + R². (2)

Từ (1),(2) ⇒ 4(R² - x²) = 3x² + R² ⇒ x² =

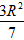
⇒ h = OO' = x√3 =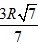

Gọi S là diện tích xung quanh và V là thể tích của hình trụ thì ta có:

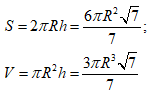
Chọn B.

Ví dụ 5 Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45⁰. Diện tích xung quanh hình trụ và thể tích V của khối trụ là:

Hướng dẫn giải:

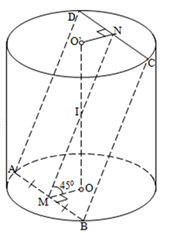
* Gọi M, N theo thứ tự là trung điểm của AB và CD.

Khi đó: OM ⊥ AB và O'N ⊥ DC

Gọi I là giao điểm của MN và OO’.
Đặt R = OA, h = OO’.

* Trong tam giác IOM vuông cân tại I nên:

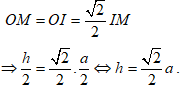
* Ta có:
R² = OA² + AM² + MO² .

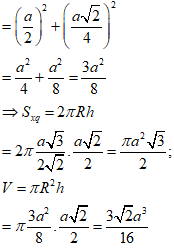
Chọn D.