Dạng bài tập hình trụ nội tiếp, ngoại tiếp hình cầu, nón, lập phương cực hay - Toán lớp 12

Dạng bài tập hình trụ nội tiếp, ngoại tiếp hình cầu, nón, lập phương cực hay

Với Dạng bài tập hình trụ nội tiếp, ngoại tiếp hình cầu, nón, lập phương cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập hình trụ nội tiếp, ngoại tiếp hình cầu, nón, lập phương từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Dùng định nghĩa hình trụ nội tiếp, ngoại tiếp của một hình

2. Ví dụ minh họa

Ví dụ 1 Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh . Thể tích của khối trụ bằng:

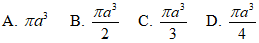
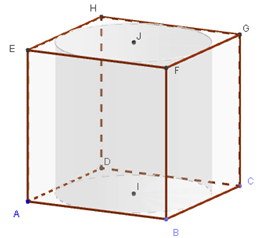
Hướng dẫn giải:

Ta có, chiều cao của hình trụ là: h = a

Đáy của hình trụ là hình tròn nội tiếp hình lập phương cạnh a nên bán kính đường tròn đáy của hình trụ là:

Khi đó, thể tích hình trụ tạo ra là:

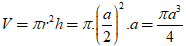
Chọn D

Ví dụ 2 Cho một hình lăng trụ tam giác đều ABC.A’B’C’ có AB= a. Biết mặt phẳng (AB’C’) hợp với mặt đáy (A’B’C’) một góc bằng 45⁰. Cho một hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ (hình trụ có các đường tròn đáy ngoại tiếp các mặt của hình lăng trụ). Tính diện tích xung quanh của hình trụ và thể tích khối trụ.

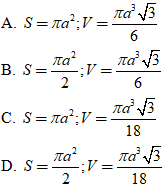
Hướng dẫn giải:

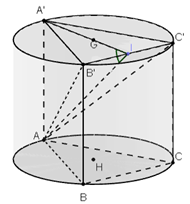
Gọi I là trung điểm B’C’.

Vì ABC.A’B’C’ là lăng trụ đều nên AI ⊥ B'C'
và A'I ⊥ B'C' .

Do đó góc giữa ( AB’C’) và (A’B’C’) là = 45⁰ .

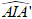
Suy ra tam giác AA’I vuông cân tại A’ nên
AA’ = A’I =

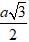
Suy ra: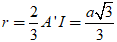

Do đó diện tích xung quanh:

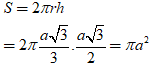
Thể tích khối trụ là: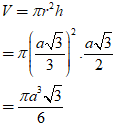

Chọn A

Ví dụ 3 Cho một hình nón đỉnh S, mặt đáy là hình tròn tâm O, bán kính R = 6cm và có thiết diện qua trục là tam giác đều. Cho một hình trụ có hai đường tròn đáy là (O; r) và (I; r), có thiết diện qua trục là hình vuông, biết đường tròn (O; r) nằm trên mặt đáy của hình nón, đường tròn (I; r) nằm trên mặt xung quanh của hình nón ( I thuộc đoạn SO). Tính thể tích khối trụ.

A. 432π(26√3 - 45) .    B. 1296π(26√3 - 45) .

C. 1296π(7 - 4√3) .    D. 432π(7 - 4√3) .

Hướng dẫn giải:

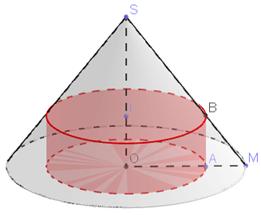
* Hình nón có bán kính đường tròn đáy
R = 6cm và có thiết diện qua trục là tam giác đều nên có

SM = 2R = 12cm, SO = SM.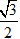 = 6√3

* Đặt SI = x, vì BI // AO nên ta có:

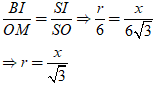
Chiều cao của hình trụ là:
h = OI = SO - SI = 6√3 - x

Do đó, thiết diện qua trục của hình trụ là hình vuông khi và chỉ khi:

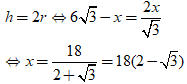
Khi đó: h = 6√3 - x = 12(2√3 - 3);
r = = 6(2√3 - 3)

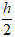
Thể tích khối trụ là:

V = πr²h
= π.[6(2√3 - 3)]².12(2√3 - 3)
= 1296π(26√3 - 45)

Chọn B.

Ví dụ 4 Cho hình trụ nội tiếp mặt cầu tâm O, biết thiết diện qua trục là hình vuông và diện tích mặt cầu bằng 72π . Tính diện tích xung quanh của hình trụ.

A. 12π    B. 16π    C. 18π    D. 36π

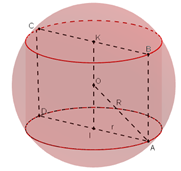
Hướng dẫn giải:

Ta có diện tích của mặt cầu là:
S_mc = 4πR² = 72π ⇔ R = 3√2

Thiết diện qua trục của hình trụ là hình vuông nên h = 2r.

Nên: R = r√2 = 3√2 ⇔ r = 3 ⇒ h= 6.

Do đó diện tích xung quanh hình trụ là:
S = 2πrh = 2π.3.6 = 36π

Chọn D.

Ví dụ 5 Một khối gỗ hình trụ có bán kính đáy
r = 10, chiều cao bằng 20. Người ta khoét rỗng khối gỗ bởi hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa hình cầu. Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ.

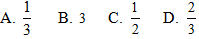
Hướng dẫn giải:

*Thể tích ban đầu của khối gỗ:

V = πr²h = π.10².20 = 2000π

* Thể tích của phần gỗ bị khoét đi là:

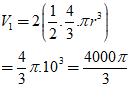
* Thể tích còn lại của khối gỗ sau khi khoét là:

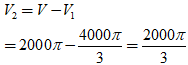
* Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ:

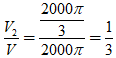
Chọn A