Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón cực hay - Toán lớp 12

Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón cực hay

Với Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Cho hình nón (H) có bán kính đường tròn đáy là R và độ dài đường sinh là l.

+ Diện tích xung quanh của hình nón bằng nửa tích số của độ dài đường tròn đáy và độ dài đường sinh:
S_xq = πR.l

+ Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện đáy:
S_tp = πR.l + πR²

+ Thể tích khối nón bằng một phần ba tích số diện tích hình tròn đáy và chiều cao:

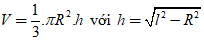
2. Ví dụ minh họa

Ví dụ 1. Cho hình nón tròn xoay có đỉnh là S; O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60⁰.Tính diện tích xung quanh của hình nón và thể tích của khối nón lần lượt là?

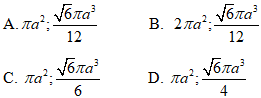
Hướng dẫn giải:

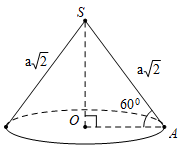
Gọi A là một điểm thuộc đường tròn đáy hình nón.

Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là
= 60⁰ .

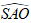
Trong tam giác vuôn SAO, ta có:

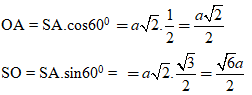
Diện tích xung quanh hình nón là:
S_xq = πRl = π.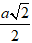 .a√2 = πR²

Thể tích của khối nón tròn xoay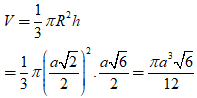
(đvtt)

Chọn A

Ví dụ 2. Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120⁰. Tính thể tích của khối nón đó theo a.

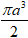
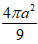
A.    B. πa³    C.    D. 2πa³

Hướng dẫn giải:

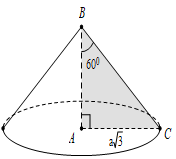
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính là:

Do góc ở đỉnh là 120⁰ nên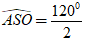

Xét tam giác SAO vuông tại O, ta có:
SO = = a

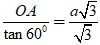
Do đó chiều cao hình nón là h = SO= a.

Vậy thể tích khối nón là
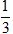
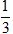
V = πr²h = π.3a².a = πa³

Chọn B.

Ví dụ 3. Một hình nón có đường sinh bằng 2a và diện tích xung quanh bằng 2πa² . Thể tích khối nón là:

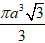
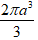
A.    B.    C. 2πa³    D. √2πa³

Hướng dẫn giải:

Ta có độ dài đường sinh là l = 2a .

Do diện tích xung quanh là 2πa² nên :

S_xq = π.R.l = 2πa² ⇒ R = = a

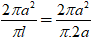
Chiều cao của hình nón là:
h = = √3a

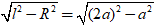
Thể tích của khối nón là
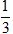
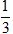
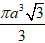
V = πR²h = π.a².√3 =

Chọn A.

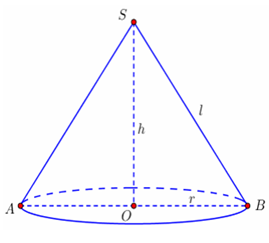
Ví dụ 4. Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 3a2. Diện tích xung quanh của (N) là:

A. 6πa²    B. √2πa²    C. 6√2πa²    D. 3√2πa²

Hướng dẫn giải:

Do cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón nên thiết diện qua trục là mặt phẳng (SAB) – với AB là đường kính của đường tròn đáy.

Theo giả thiết tam giác SAB là tam giác vuông cân tại S và có diện tích 3a² nên

S_ABC = 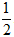SA² = 3a² ⇒ SA = √6a

Khi đó, độ dài đường sinh của hình nón là

l = SA = √6a

Do tam giác SAB là tam giác vuông cân tại S nên
AB = SA.√2 = √6a.√2 = 2√3a

Suy ra, đường cao của hình nón là:

h = SO = AB/2 = √3a

Bán kính đường tròn đáy là R = AB/2 = a√3 .

Diện tích xung quanh của (N) là:

S_xq = π.R.l = π.a√3.a.√6 = 3√2πa²

Chọn D

Ví dụ 5. Cho hình tròn có bán kính bằng 6. Cắt bỏ 1/4 hình tròn giữa hai bán kính OA và OB, rồi ghép hai bán kính đó lại sao cho hình thành một hình nón ( hình vẽ ). Tính thể tích khối nón tương ứng

Hướng dẫn giải:

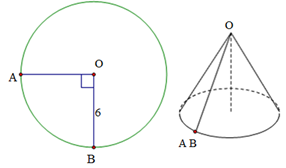
Diện tích hình tròn có bán kính bằng R = 6 là: S_tron = πR² = π6² = 36π

Cắt bỏ 1/4 hình tròn thì diện tích còn lại chính là diện tích xung quanh của nón. Đường sinh của nón là bán kính đường tròn: l = R = 6

Diện tích xung quanh của nón là:
S_xq = S_tron = .36π = 27π (1)

Lại có: S_xq = π.r.l = π.r.6 (2)

Từ (1) và (2) suy ra: π.r.6 = 27π ⇒ r =

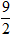
Khi đó, đường cao hình nón là:

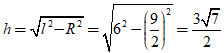
Thể tích khối nón tương ứng là:

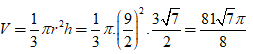
Chọn A.