Dạng bài tập về hình trụ, mặt trụ cực hay, có lời giải - Toán lớp 12

Dạng bài tập về hình trụ, mặt trụ cực hay, có lời giải

Với Dạng bài tập về hình trụ, mặt trụ cực hay, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về hình trụ, mặt trụ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

+ Cho đường thẳng ∆. Xét một đường thẳng
l// ∆, cách ∆ một khoảng bằng R. Mặt tròn xoay sinh bởi đường thẳng l như thế khi quay quanh ∆ được gọi là mặt trụ.

+ Cắt mặt trụ T trục ∆ , bán kính R bởi hai mặt phẳng phân biệt (P) và (P’) cùng vuông góc với ∆, ta được giao tuyến là hai đường tròn(C) và (C’). Phần măt trụ T nằm giữa hai mp (P) và (P’) cũng với hai hình tròn xác định bởi (C) và (C’) được gọi là hình trụ.

2. Ví dụ minh họa

Ví dụ 1 Cho hình chữ nhật ABCD cạnh AB = 6; AD = 4 quay quanh AB ta được hình trụ có diện tích xung quanh bằng:

A. S_xq = 8π .    B. S_xq = 48π .

C. S_xq = 50π .    D. S_xq = 32π .

Hướng dẫn giải:

Khi quay hình chữ nhật quanh cạnh AB ta được hình trụ có chiều cao h = AB = 6, bán kính đường tròn đáy là R = AD = 4.

Do đó, diện tích xung quanh của hình trụ là:

S = 2πR.h = 2π.4.6 = 48π

Chọn B.

Ví dụ 2 Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó

A. S_tp = 4π.    B. S_tp = 2π .

C. S_tp = 6π .    D. S_tp = 10π .

Hướng dẫn giải:

Khi quay hình chữ nhật quanh trục MN ta được hình trụ có:

+ chiều cao: h = AB = 1 .

+ bán kính đường tròn đáy là r = 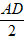= 1

Do đó,diện tích toàn phần của hình trụ đó là:

S_tp = 2πrh + 2πr² = 2π.1.1 + 2π.1² = 4π

Chọn A.

Ví dụ 3 Một hình thang vuông ABCD có đường cao AD = π, đáy nhỏ AB = π , đáy lớn CD = 2π . Cho hình thang quay quanh CD, ta được khối tròn xoay có thể tích bằng

A. V = 2π⁴ .    B. V = 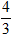π⁴ .

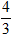
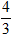
C. V = π³ .    D. V = π² .

Hướng dẫn giải:

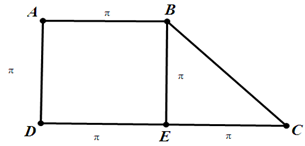
Khi quay hình thang quanh CD ta được khối tròn xoay gồm 2 phần:

+ Khối V₁ là khối trụ có bán kính đáy AD = π và chiều cao AB = π nên thể tích khối trụ tạo thành là:
V₁ = π.π².π = π⁴

+ Khối V₂ là khối nón có bán kính đường tròn đáy là BE = π và đường cao BC = π nên thể tích của khối nón là:
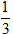
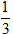
V₂ = .π.π².π = .π⁴

Vậy thể tích khối tròn xoay cần tính là :
V = V₁ + V₂ = 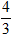π⁴

Chọn B.

Ví dụ 4 Cho hình chữ nhật ABCD có AB = nAD. Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD ta được khối trụ có diên tích toàn phần là S₁, khi quay hình chữ nhật ABCD một vòng quanh cạnh AD ta được khối trụ có diên tích toàn phần là S₂. Khẳng định nào sau đây là đúng?

A. nS₁ = S₂    B. S₁ = nS₂.

C. S₁ = ( n+ 1).S₂.    D. S₂ = (n+1)S₁

Hướng dẫn giải:

* Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD ta được khối trụ có bán kính
r₁ = AD; h₁ = AB

* Khi đó
S₁ = 2π.AD.AB + 2π.AD²
= 2π(nAD² + AD²)

* Tương tự khi quay hình chữ nhật ABCD một vòng quanh cạnh AD ta có:
r₂ = AB; h₂ = AD

* Khi đó S₂ = 2π(nAD² + n²AD)

Do đó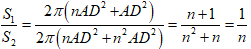
.

Suy ra: nS₁ = S₂

Chọn A.

Ví dụ 5 Cho hình chữ nhật ABCD với AB = 1,
BC = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), song song AD và cách AD một khoảng 2 ; đồ thị không có điểm chung với hình chữ nhật ABCD. Tính thể tích khối tròn xoay tạo được khi quay hình chữ nhật ABCD quanh d.

A. 15π .    B. 27π .    C. 12π .    D. 10π

Hướng dẫn giải:

* BC cách đường d một khoảng d’ = 2+ AB = 3

*Do đó khối tròn xoay là tập hợp các điểm nằm ở giữa hai hình trụ có bán kính lần lượt là 2 và 3, chiều cao của hai hình trụ đều là 3.

Thể tích khối tròn xoay bằng hiệu thể tích của hai khối trụ nêu trên là:

V = 3².3.π - 2².3.π = 15π

Chọn A.