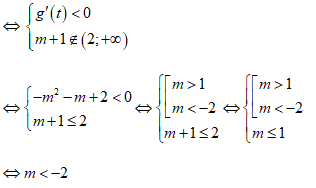Cách xét tính đơn điệu của hàm logarit cực hay, có lời giải - Toán lớp 12

Cách xét tính đơn điệu của hàm logarit cực hay, có lời giải

Với Cách xét tính đơn điệu của hàm logarit cực hay, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính đơn điệu của hàm logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

- Phương pháp chung:

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

- Dựa vào tính đơn điệu của hàm số mũ:

Cho hàm số y = log_a⁡x,(a > 0; a ≠ 1) xác định trên (0;+∞) Khi đó:

Nếu a > 1 thì hàm số đồng biến trên (0;+∞)

Nếu 0 < a < 1 thì hàm số nghịch biến trên (0;+∞)

B. Ví dụ minh họa

Ví dụ 1: Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?

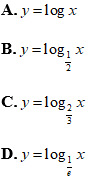
Lời giải

Chọn A

Ta có 10 > 1 nên hàm số y⁡= log⁡x đồng biến trên tập xác định là (0;+∞)

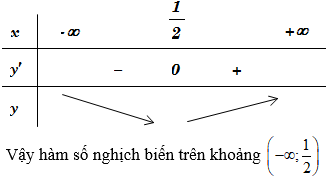
Ví dụ 2: Hàm số y = ln⁡(x² - x + 1) nghịch biến trên những khoảng nào sau đây?

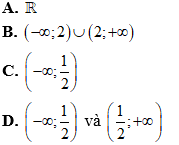
Lời giải

Chọn C

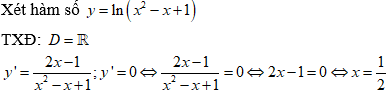
Bảng biến thiên:

Ví dụ 3: Tìm tất cả các giá trị của tham số để hàm số y = log_{a² - 3a + 3}⁡x đồng biến trên (0;+∞)

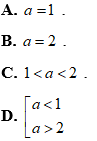
Lời giải

Chọn D

Hàm số đồng biến trên (0;+∞) ⇔ 1 < a² - 3a + 3 ⇔ a² - 3a + 2 > 0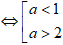

C. Bài tập trắc nghiệm

Bài 1: Cho hàm số 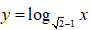. Phát biểu nào sau đây là đúng?

A. Hàm số nghịch biến trên (0;+∞)

B. Hàm số đồng biến trên khoảng (0;+∞)

C. Hàm số đồng biến trên khoảng R

D. Hàm số luôn dương với mọi x > 0

Lời giải:

Chọn A

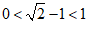
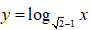
Do nên hàm số nghịch biến trên tập xác định là (0;+∞)

Bài 2: Hàm số nào dưới đây đồng biến trên tập xác định của nó?

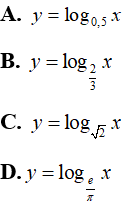
Lời giải:

Chọn C

Do 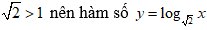đồng biến trên tập xác định là (0;+∞)

Bài 3: Hàm số nào dưới đây nghịch biến trên tập xác định của nó?

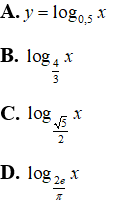
Lời giải:

Chọn A

Do 0 < 0,5 < 1 nên hàm số 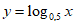nghịch biến trên tập xác định là (0;+∞)

Bài 4: Trong các hàm số sau,hàm số nào đồng biến trên tập xác định của nó?

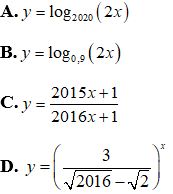
Lời giải:

Chọn A

Xét hàm số y = log_2020⁡(2x) xác định trên (0;+∞)

Ta có 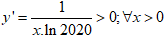nên hàm số đồng biến trên (0;+∞)

Bài 5: Hàm số y = x².ln⁡x đồng biến trên khoảng nào?

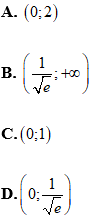
Lời giải:

Chọn B

Bài 6: Cho bốn hàm số sau 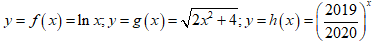và y = l(x) = ln⁡(x² + 1). Có bao nhiêu hàm số đồng biến trên khoảng (0;+∞).

A. 1

B. 2

C. 3

D. 4

Lời giải:

Chọn C

Hàm số y = ln⁡x có cơ số e > 1 nên đồng biến trên (0;+∞)

Hàm số 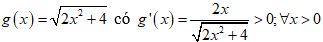nên đồng biến trên (0;+∞)

Hàm số 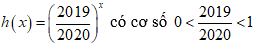nên nghịch biến trên R

Hàm số 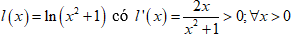nên đồng biến trên (0;+∞)

Bài 7: Với điều kiện nào của a thì hàm số y = log_{a² - a + 1}⁡x đồng biến trên (0;+∞)

A. a ∈ (0;1)

B. a ∈ (-∞;0)∪(1+∞)

C. a ≠ 0; a ≠ 1

D. a ∈ R

Lời giải:

Chọn B

Hàm số đã cho xác định trên (0;+∞)

Hàm số đồng biến trên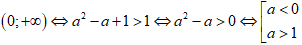

Bài 8: Biết tập các giá trị thực của a để hàm số y = log_{a² + a + 1}⁡x nghịch biến trên tập xác định là khoảng (m;n). Tính S = 2m + n.

A. S = -2

B. S = 0

C. S = 1

D. S = 2

Lời giải:

Chọn A

Hàm số y = (a² + a + 1)^x xác định trên (0;+∞)

Hàm số nghịch biến trên (0;+∞) ⇔ 0 < a² + a + 1 < 1 ⇔ a² + a < 0 ⇔ -1 < a < 0

Nên m = -1 ; n = 0 ⇒ S = 2m + n = -2 .

Bài 9: Biết khoảng nghịch biến của hàm số 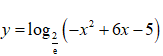là khoảng (a;b) với a, b ∈ R. Giá trị biểu thức T = 4a - b bằng:

A. 1.

B. 0.

C. -1.

D. 2.

Lời giải:

Chọn A

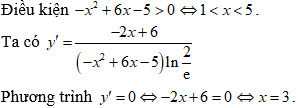
Bảng biến thiên

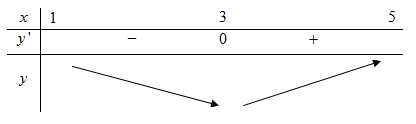
Từ bảng biến thiên ta có hàm số nghịch biến trên (1;3). Vậy T = 4a - b = 4.1 - 3 = 1

Bài 10: Tìm tất cả các giá trị thực của tham số m để hàm số 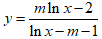nghịch biến trên (e²;+∞).

A. m ≤ -2 hoặc m = 1.

B. m < -2 hoặc m = 1.

C. m < -2.

D. m < -2 hoặc m > 1.

Lời giải:

Chọn C

Đặt t = ln⁡x, ta biết rằng hàm số f(x) = ln⁡x đồng biến trên (e²;+∞) ⇒ t > ln⁡e² =2.

Xét hàm số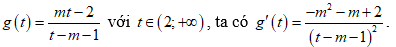

Vậy hàm số ban đầu nghịch biến trên (e²;+∞) ⇔ hàm số g(t) nghịch biến trên (2;+∞)