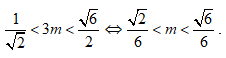Cách xét tính đơn điệu của hàm số chứa căn thức cực hay, có lời giải - Toán lớp 12

Cách xét tính đơn điệu của hàm số chứa căn thức cực hay, có lời giải

Với Cách xét tính đơn điệu của hàm số chứa căn thức cực hay, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính đơn điệu của hàm số chứa căn thức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Tìm khoảng đồng biến của hàm số .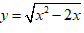

A. (0;+∞)

B. (2;+∞)

C. (-∞;0)

D. (0;2)

Lời giải

Chọn B

Hàm số đã cho xác định khi: 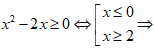Tập xác định: D = (-∞;0]∪[2;+∞).

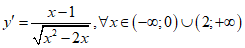
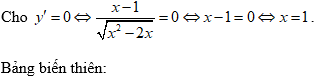
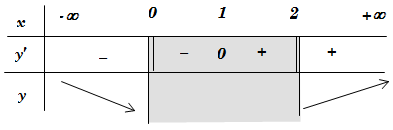
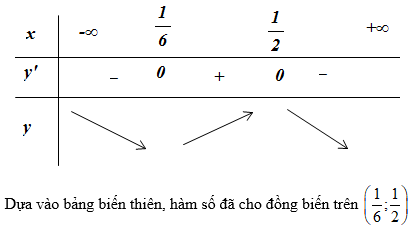
Ta có: . Hàm số không có đạo hàm tại: x = 0; x = 2.

Dựa vào bảng biến thiên, hàm số đồng biến trên (2;+∞).

Ví dụ 2: Tìm khoảng đồng biến của hàm số .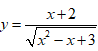

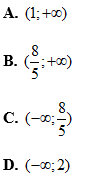
Lời giải

Chọn C

Hàm số đã cho xác định khi: x² - x + 3 > 0 đúng ∀ x ∈ R.

Hàm số đã cho xác định trên D = R

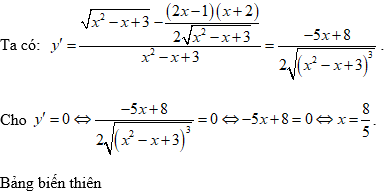
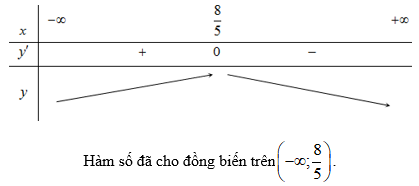
Ví dụ 3: Tìm khoảng đồng biến của hàm số .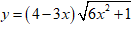

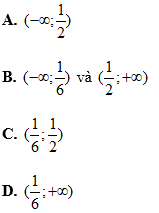
Lời giải

Chọn C

Hàm số đã cho xác định trên D = R.

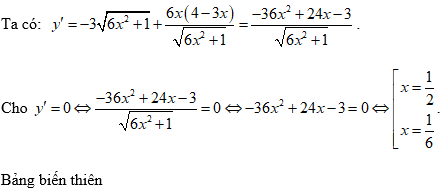
C. Bài tập trắc nghiệm

Bài 1: Hàm số 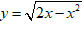nghịch biến trên khoảng nào.

A. (0;1).

B. (-∞;1).

C. (1;2).

D. (1;+∞).

Lời giải:

Chọn C

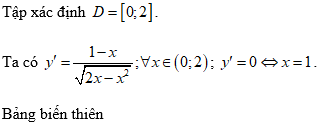
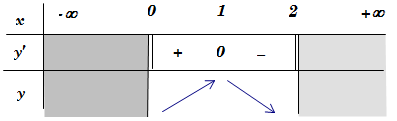
Vậy hàm số nghịch biến trên khoảng (1;2)

Bài 2: Cho hàm 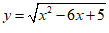. Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng (5;+∞).

B. Hàm số đồng biến trên khoảng (3;+∞).

C. Hàm số đồng biến trên khoảng (-∞;1).

D. Hàm số nghịch biến trên khoảng (-∞;3).

Lời giải:

Chọn A

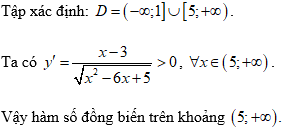
Bài 3: Cho hàm số 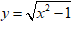. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng (0;+∞).

B. Hàm số đồng biến trên (-∞;+∞)

C. Hàm số đồng biến trên khoảng (1;+∞).

D. Hàm số nghịch biến trên khoảng (1;+∞).

Lời giải:

Chọn C

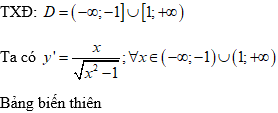
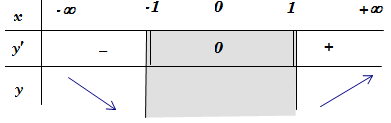
Vậy hàm số đồng biến trên khoảng (1;+∞).

Bài 4: Hỏi hàm số 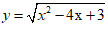đồng biến trên khoảng nào?

A. (2;+∞)

B. (-∞;3)

C. (-∞;1)

D. (3;+∞)

Lời giải:

Chọn D

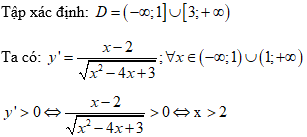
Kết hợp với điều kiện xác định của hàm số, suy ra khoảng đồng biến của hàm số là (3;+∞)

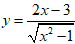
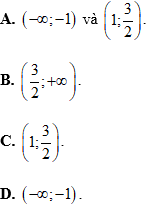
Bài 5: Hàm số nghịch biến trên khoảng nào trong các khoảng dưới đây?

Lời giải:

Chọn D

Bài 6: Tìm khoảng nghịch biến của hàm số ?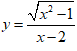

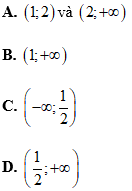
Lời giải:

Chọn C

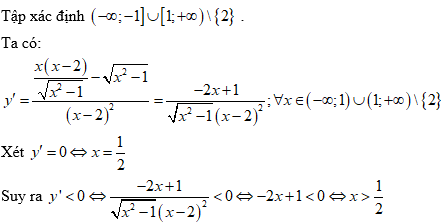
Kết hợp với điều kiện ta có hàm số nghịch biến trên các khoảng (1;2) và (2;+∞)

Bài 7: Cho hàm số 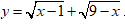. Chọn mệnh đề đúng?

A. Hàm số đồng biến trên khoảng (5;9)

B. Hàm số nghịch biến trên khoảng (5;9)

C. Hàm số đồng biến trên khoảng (1;9)

D. Hàm số nghịch biến trên khoảng (1;9)

Lời giải:

Chọn B

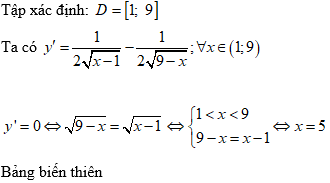
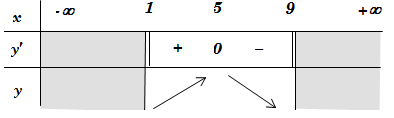
Vậy hàm số nghịch biến trong khoảng (5;9)

Bài 8: Hàm số nào sau đây là hàm số đồng biến trên R?

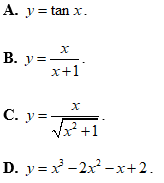
Lời giải:

Chọn C

Hàm số y = tan⁡x đồng biến trên mỗi khoảng 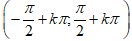, k ∈ Z. Nên loại A.

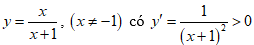
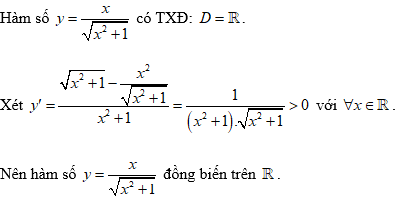
Hàm số với ∀ x ≠ -1 nên loại B.

Bài 9: Hàm số nào sau đây đồng biến trên R?

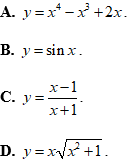
Lời giải:

Chọn D

+) Loại đáp án A: y = x⁴ -x³ + 2x. TXĐ: D = R. y' = 4x³ - 3x² + 2 = 0 (*).

Phương trình (*) luôn có một nghiệm nên hàm số không đồng biến trên R.

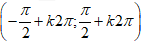
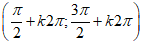
+) Loại đáp án B: y = sin⁡x luôn đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng nên hàm số không đồng biến trên R.

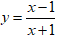
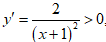
+) Loại đáp án C: . TXĐ: D = R{-1}. ∀ x ≠ -1 ⇒ hàm số luôn đồng biến trên từng khoảng xác định (-∞;-1) và (-1;+∞).

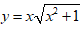
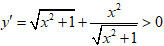
+) Chọn đáp án D: . TXĐ: D = R. ∀ x ∈ R

⇒ hàm số luôn đồng biến trên R.

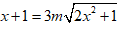
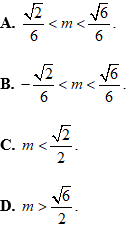
Bài 10: Tìm tất cả các giá trị thực của m để phương trình có hai nghiệm thực phân biệt.

Lời giải:

Chọn A

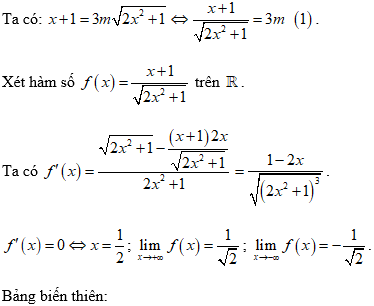
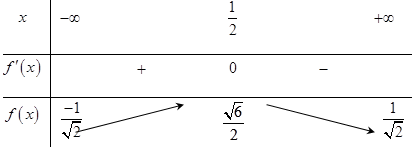
Dựa vào bảng biến thiên ta có phương trình (1) có hai nghiệm thực phân biệt khi và chỉ khi