Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn AM^2 + BM^2= CM ^2
Câu hỏi:
Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
Trả lời:
Chọn A
<=> Mặt cầu
Câu hỏi:
Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
Trả lời:
Chọn A
<=> Mặt cầu
Câu 1:
Cho đường tròn (C) đường kính AB và đường thẳng . Để hình tròn xoay sinh bởi (C) khi quay quanh là một mặt cầu thì cần có thêm điều kiện nào sau đây:
(I) Đường kính AB thuộc .
(II) cố định và đường kính AB thuộc .
(III) cố định và hai điểm A, B cố định trên .
Câu 2:
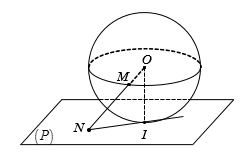
Câu 3:
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
Câu 4:
Câu 5:
Cho tứ diện OABC với A(-4,0,0); B(0,6,0); C(0,0,-8). Mặt cầu (S) ngoại tiếp từ diện có tâm và bán kính là:
