Cho các số phức z thỏa mãn |z – 2 – 4i| = 2
Câu hỏi:
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
A. 8i
B. 4
C. -8
D. 8
Trả lời:
Chọn D.
Ta có 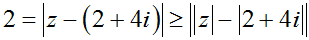
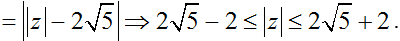
+ Giá trị lớn nhất của |z| là 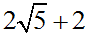 đạt được tại
đạt được tại
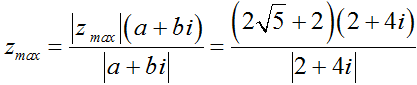
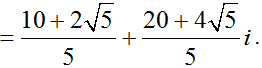
+ Giá trị nhỏ nhất của |z| là 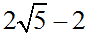 , đạt được tại
, đạt được tại
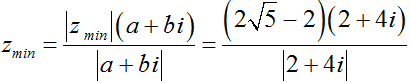
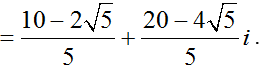
Vậy tổng phần ảo là: 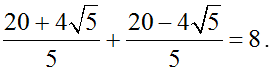
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
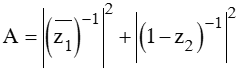
Xem lời giải »
Câu 2:
Gọi z1; z2 lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức 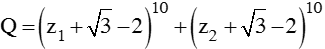
Xem lời giải »
Câu 3:
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Xem lời giải »
Câu 4:
Cho số phức z1; z2 thỏa mãn 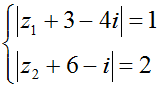 . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?
. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?
Xem lời giải »
đạt được tại
, đạt được tại

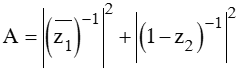
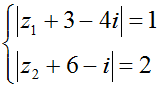 . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?
. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?