Cho hàm số f(x) = 1/x^2 +1. Khi đó, nếu đặt x=tant thì
Câu hỏi:
Cho hàm số . Khi đó, nếu đặt x=tant thì:
A.
B.
C.
D.
Trả lời:
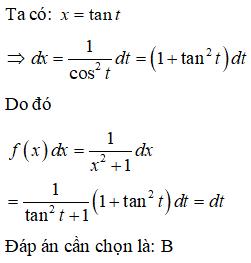
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số y = f(x) có f’(x) liên tục trên nửa khoảng thỏa mãn biết . Giá trị bằng:
Xem lời giải »
Câu 2:
Cho hàm số f(x) liên tục trên R và . Tính tích phân
Xem lời giải »
Câu 3:
Biết với m, n, p là các số nguyên dương. Tính tổng S = m + n + p
Xem lời giải »
Câu 4:
Cho y = f(x) là hàm số chẵn và liên tục trên R. Biết . Giá trị của bằng:
Xem lời giải »
Câu 5:
Biết F(x) là một nguyên hàm của hàm số thỏa mãn F(2)=0. Khi đó phương trình F(x)=x có nghiệm là:
Xem lời giải »
Câu 6:
Biết F(x) là một nguyên hàm của hàm số thỏa mãn . Giá trị của là:
Xem lời giải »
Câu 7:
Nếu đặt x=sint thì nguyên hàm có dạng với a, b thuộc Z. tính tổng S = a + b
Xem lời giải »
Câu 8:
Cho hàm số , nếu đặt , với thì bằng
Xem lời giải »
