Cho hình bình hành ABCD có góc bad = 60 độ ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD. a) MCND là hình thoi. b) ABMD là hình thang cân.
Câu hỏi:
Cho hình bình hành ABCD có ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.
a) MCND là hình thoi.
b) ABMD là hình thang cân.
Trả lời:
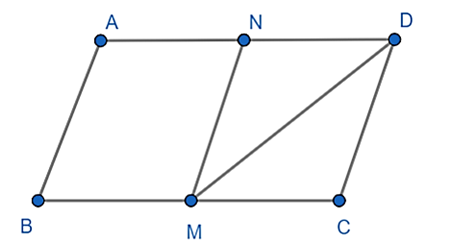
a) Ta có: BM = MC vì M là trung điểm BC
AN = ND vì N là trung điểm AD
Nên MN là đường trung bình ABCD
Suy ra: MN // AB // CD
Lại có: BC = AD, nên BM = AN
Xét ABMN có: BM // AN và BM = AN nên ABMN là hình bình hành
Suy ra: MN = AB
Mà AB = CD nên MN = CD
Lại có: AD = BC = 2AB nên ND = MC = AB = CD = MN
Vậy MNDC là hình thoi
b) Xét tứ giác BMDA có: BM // AD nên BMAD là hình thang
Vì MNDC là hình thoi nên MC = CD
Nên tam giác MCD cân tại C
Mà:
Nên tam giác MCD đều
Suy ra: MC = CD = MD
Mà CD = AB nên MD = Ba
Vậy BMDA là hình thang cân.

