Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.
Câu hỏi:
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.
Trả lời:
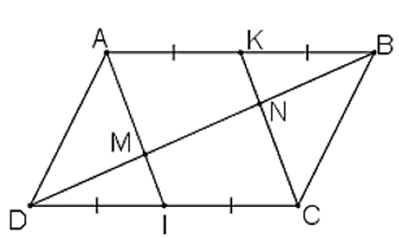
a) ABCD là hình bình hành
⇒ AB // CD ⇒ AB // IC
AB = CD
Mà K, I lần lượt là trung điểm của AB và CD.
⇒AK = IC
Mà AK // IC
⇒ AKIC là hình bình hành
Xét ΔADI và ΔBCKcó:
DI = BK
AI = CK
AD = BC
⇒ ΔADI = ΔBCK (c.c.c)
⇒
Xét ΔADM và ΔCBN có:
AD=BC
(Do AD // BC)
⇒ ΔADM = ΔCBN (g.c.g).

