Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng
Câu hỏi:
Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.
Tìm giao tuyến của hai mặt phẳng
a) (SBM) và (SCD);
b) (ABM) và (SCD);
c) (ABM) và (SAC).
Trả lời:
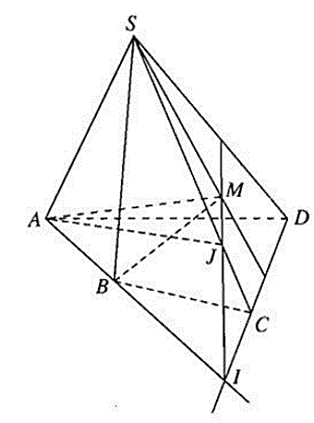
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên (SBM) ∩ (SCD) = SM
b) M là điểm chung thứ nhất của (AMB) và (SCD)
Gọi I = AB ∩ CD
Ta có: I ∈ AB ⇒ I ∈ (ABM)
Mặt khác: I ∈ CD ⇒ I ∈ (SCD)
Nên (AMB) ∩ (SCD) = IM.
c) Gọi J = IM ∩ SC.
Ta có: J ∈ SC ⇒ J ∈ (SAC) và J ∈ IM ⇒ J ∈ (ABM).
Hiển nhiên A ∈ (SAC) và A ∈ (ABM)
Vậy (SAC) ∩ (ABM) = AJ.

