Cho hình bình hành ABCD hai đường chéo không vuông góc với
Câu hỏi:
Cho hình bình hành ABCD hai đường chéo không vuông góc với nhau. Vẽ điểm E đối xứng với A qua BD. Chứng minh rằng 4 điểm B, C, E, D là 4 đỉnh của hình thang cân.
Trả lời:
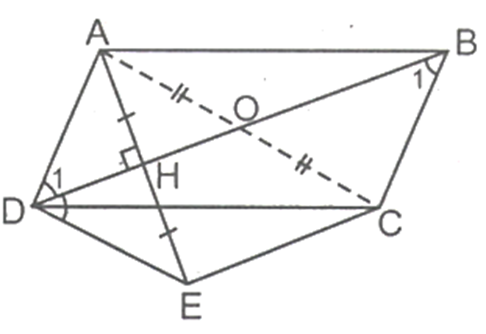
Gọi O là giao điểm của AC và BD, H là giao điểm BD và AE.
Vì E đối xứng với A qua BD nên H là trung điểm của AE.
Xét tam giác ACE có OH là đường trung bình nên OH // CE (O là trung điểm AC, H là trung điểm AE)
Vậy BCED là hình thang.
Xét tam giác ADH và tam giác DHE có:
Chung DH
\(\widehat {AHD} = \widehat {DHE} = 90^\circ \)
AH = HE
Nên: ∆ADH = ∆EDH (c.g.c)
Suy ra: \(\widehat {BDE} = \widehat {{D_1}}\)
Mà ABCD là hình bình hành nên: \(\widehat {{B_1}} = \widehat {{D_1}}\) (2 góc so le trong)
Lại có: \(\widehat {BDE} = \widehat {{B_1}}\left( { = \widehat {{D_1}}} \right)\)
Vậy BCED là hình thang cân.

