Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc
Câu hỏi:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.
A. V =
B. V =
C. V =
D. V =
Trả lời:
Chọn D
Thể tích khối chóp S. ABCD là:
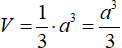
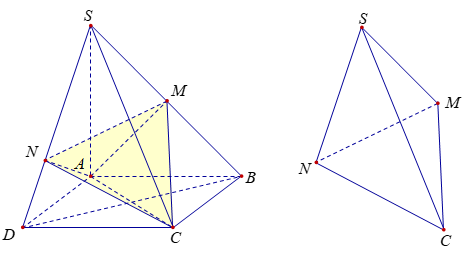
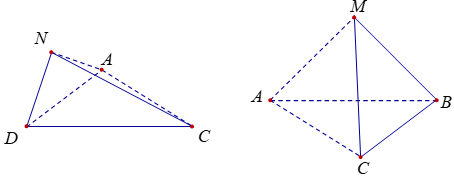
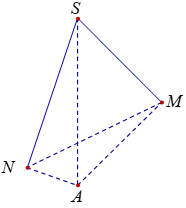
Thể tích tứ diện SMNC là:
 .
.
Thể tích tứ diện NACD là:
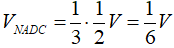 .
.
Thể tích tứ diện MABC là:
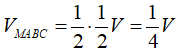 .
.
Thể tích tứ diện SAMN là:
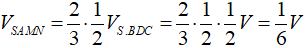 .
.
Mặt khác ta có:
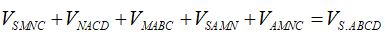
Suy ra:
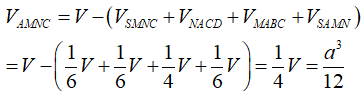
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
Xem lời giải »
Câu 2:
Cho hình chóp tứ giác đều S. ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng (SCD), cắt đường thẳng SD tại E. Gọi V và V₁ lần lượt là thể tích các khối chóp S.ABCD và D.ACE. Tính số đo góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD biết V = 5
Xem lời giải »
Câu 3:
Cho hình chóp S. ABC, có AB=5 (cm), BC=6 (cm), AC=7 (cm). Các mặt bên tạo với đáy 1 góc 600. Thể tích của khối chóp bằng:
Xem lời giải »
Câu 4:
Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng a/2. Thể tích của khối lăng trụ bằng:
Xem lời giải »
Câu 5:
Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:
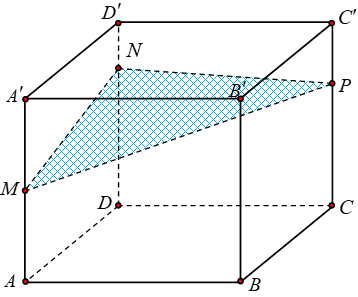
Xem lời giải »
Câu 6:
Xét tứ diện ABCD có các cạnh AB=BC=CD=DA=1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng:
Xem lời giải »
Câu 7:
Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂.
Xem lời giải »
Câu 8:
Xét tứ diện ABCD có các cạnh AC=CD=DB=BA=2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng:
Xem lời giải »
.
.
.
.


