Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng (alpha) đi qua
Câu hỏi:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng (α) đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số \(\frac{{SN}}{{S{\rm{D}}}}\) để (α) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{{\sqrt 5 - 1}}{2}\)
D. \(\frac{{\sqrt 3 - 1}}{2}\).
Trả lời:
Đáp án đúng là: C
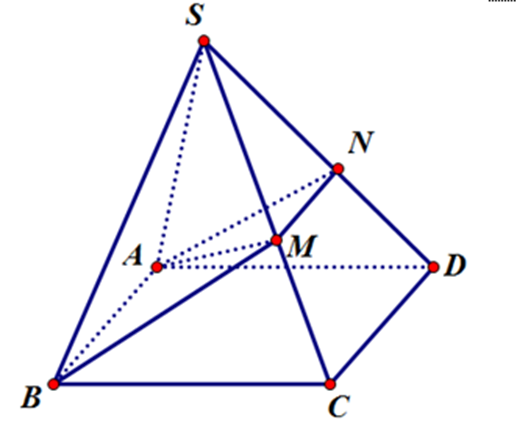
Ta có (α) ∩ (SCD) = NM nên NM // CD
Do đó (α) là (ABMN)
Mặt phẳng (α) chia khối chóp thành 2 phần có thể tích bằng nhau là
\({V_{S.ABMN}} = {V_{ABCDNM}} \Rightarrow {V_{S.ABMN}} = \frac{1}{2}.{V_{S.ABCD}}\) (1)
Ta có: \({V_{S.ABC}} = {V_{S \cdot ACD}} = \frac{1}{2} \cdot {V_{S \cdot ABCD}}\)
Đặt \(\frac{{SN}}{{SD}} = x\) với \((0 < x < 1)\), khi đó theo Ta – let ta có \(\frac{{SN}}{{SD}} = \frac{{SM}}{{SC}} = x\)
Mặt khác \(\frac{{{V_{S.ABM}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SB}}{{SB}}.\frac{{SM}}{{SC}} = x\)
Suy ra \({V_{S.ABM}} = \frac{x}{2}{V_{S.ABC{\rm{D}}}}\)
Ta có: \(\frac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \frac{{SA}}{{SA}}.\frac{{SN}}{{SD}}.\frac{{SM}}{{SC}} = {x^2}\)
Suy ra \({V_{S.AMN}} = \frac{{{x^2}}}{2}{V_{S.ABC{\rm{D}}}}\)
Ta có: \({V_{S.ABMN}} = {V_{S.AMB}} + {V_{S.AMN}} = \left( {\frac{x}{2} + \frac{{{x^2}}}{2}} \right){V_{S.ABC{\rm{D}}}}\) (2)
Từ (1) và (2) suy ra
\(\begin{array}{l}\frac{x}{2} + \frac{{{x^2}}}{2} = \frac{1}{2}\\ \Leftrightarrow {x^2} + x - 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 1 - \sqrt 5 }}{2}\\x = \frac{{ - 1 + \sqrt 5 }}{2}\end{array} \right.\end{array}\)
Mà \((0 < x < 1)\) nên \(x = \frac{{\sqrt 5 - 1}}{2}\)
Hay \(\frac{{SN}}{{S{\rm{D}}}} = \frac{{\sqrt 5 - 1}}{2}\)
Vậy ta chọn đáp án C.

