Cho hình chữ nhật ABCD. Qua B kẻ đường thẳng vuông góc với
Câu hỏi:
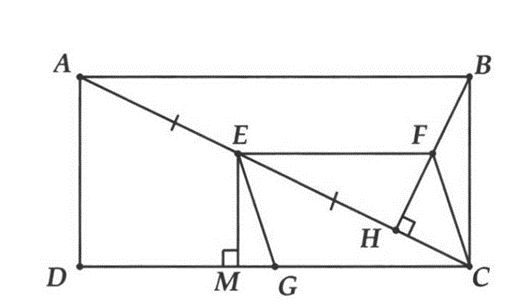
Cho hình chữ nhật ABCD. Qua B kẻ đường thẳng vuông góc với đường chéo AC tại H. Gọi E, F, G theo thứ tự là trung điểm của AH, BH, CD.
a, Chứng minh tứ giác EFCG là hình bình hành.
b, Chứng minh \(\widehat {BEG} = 90^\circ \).
c, Cho biết BH = 4 cm, \(\widehat {BAC} = 30^\circ \). Tính SABCD; SEFCG.
Trả lời:
a) Vì E, F theo thứ tự là trung điểm của AH, BH nên EF là đường trung bình trong tam giác ABH
⇒ EF // AB và EF = \(\frac{1}{2}AB = \frac{1}{2}DC = DG\)
Vì AB // DG nên EF // DG
Xét tứ giác EFCG có: EF // DG và EF = DG
Nên EFCG là hình bình hành
b) Lại có: AB ⊥ BC mà EF // AB nên EF ⊥ BC
Mà BF ⊥ AC
Xét trong tam giác BEC có: EF ⊥ BC; BF ⊥ EC nên F là trực tâm của tam giác BEC
Suy ra: CF ⊥ BE (1)
Mà theo phần a có EFCG là hình bình hành nên: EG // CF (2)
Từ (1) và (2): EG ⊥ BE hay \(\widehat {BEG} = 90^\circ \)
c) Sử dụng tỉ số sinA trong tam giác vuông HAB ta có:
\(\sin \widehat A = \frac{{BH}}{{AB}} \Rightarrow AB = \frac{4}{{\sin 30^\circ }} = 8cm\)
\(\tan \widehat A = \frac{{BC}}{{AB}} = \frac{{\sqrt 3 }}{3}\)⇒ \(BC = \frac{{8\sqrt 3 }}{3}\)
AC = \(\sqrt {A{B^2} + B{C^2}} = \frac{{16\sqrt 3 }}{3}\)
Lại có: AB2 = AH.AC ⇒ AH = AB2 : AC = 4\(\sqrt 3 \)
HC = AC – AH = \(\frac{{16\sqrt 3 }}{3} - 4\sqrt 3 = \frac{{4\sqrt 3 }}{3}\)
Mà AE = EH = \(\frac{1}{2}AH = 2\sqrt 3 \)
Suy ra: EC = HC + EH = \(\frac{{4\sqrt 3 }}{3} + 2\sqrt 3 = \frac{{10\sqrt 3 }}{3}\)
Kẻ EM vuông góc với CD tại M
Có \(\widehat {BAC} = \widehat {ACD} = 30^\circ \)(2 góc so le trong)
Ta có: sin\(\widehat {ACD} = \sin 30^\circ = \frac{{EM}}{{EC}}\)
⇒ EM = \(\sin 30^\circ .\frac{{10\sqrt 3 }}{3} = \frac{{5\sqrt 3 }}{3}\)
SABCD = AB.BC = \(8.\frac{{8\sqrt 3 }}{3} = \frac{{64\sqrt 3 }}{3}\left( {c{m^2}} \right)\)
SEFCG = EM.EF = EM . \(\frac{1}{2}AB = \frac{{5\sqrt 3 }}{3}.\frac{1}{2}.8 = \frac{{20\sqrt 3 }}{3}\left( {c{m^2}} \right)\).

