Cho hình lăng trụ đứng ABC.A1B1C1 có AB = a, AC = 2a, AA1 = 2a
Câu hỏi:
Trả lời:
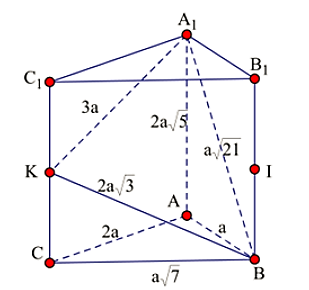
Ta có: \[BC = \sqrt {A{C^2} + A{B^2} - 2.AC.AB.\cos 120^\circ } = a\sqrt 7 \]
A1B = \(\sqrt {{A_1}{A^2} + A{B^2}} = a\sqrt {21} \)
A1K = \(\sqrt {{A_1}{C_1}^2 + {C_1}{K^2}} = 3a\)
KB = \(\sqrt {K{C^2} + C{B^2}} = 2a\sqrt 3 \)
d(I; (A1BK)) = \(\frac{1}{2}\)d(B1; (A1BK)) = \(\frac{1}{2}.\frac{{3{V_{{B_1}{A_1}AK}}}}{{{S_{\Delta {A_1}BK}}}}\)
Mà \[{V_{{B_1}{A_1}AK}} = \frac{1}{2}{V_{K.{A_1}{B_1}BA}} = \frac{1}{2}.\frac{2}{3}.{V_{ABC.{A_1}{B_1}{C_1}}} = \frac{1}{3}.2a\sqrt 5 .\frac{1}{2}.a.2a.\sin 120^\circ = \frac{{{a^3}\sqrt {15} }}{3}\]
Theo công thức Herong, diện tích tam giác A1BK bằng:
\(S = \sqrt {p\left( {p - 2a\sqrt 3 } \right)\left( {p - 3a} \right)\left( {p - a\sqrt {21} } \right)} = 3{a^2}\sqrt 3 \) với \(p = \frac{{2a\sqrt 3 + 3a + a\sqrt {21} }}{2}\)
Vậy d(I, (A1BK)) = \(\frac{3}{2}.\frac{{\frac{{{a^3}\sqrt {15} }}{3}}}{{3{a^2}\sqrt 3 }} = \frac{{a\sqrt 5 }}{6}\).

