Cho hình thang cân ABCD có CD = 2AB = 12cm, chu vi tam giác ACD là 25cm. Chu vi tam giác ABC là ...cm.
Câu hỏi:
Cho hình thang cân ABCD có CD = 2AB = 12cm, chu vi tam giác ACD là 25cm. Chu vi tam giác ABC là ...cm.
Trả lời:
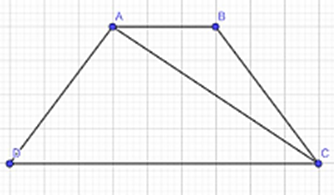
Ta có: 2AB = 12 ⇒ AB = 6
ABCD là hình thang cân ⇒ BC = AD
PACD = 25 ⇒ AC + CD + DA = 25 ⇒ AC + AD = 25 – CD = 25 – 12 = 13
Suy ra: AC + BC = 13.
⇒ PABC = AB + BC + CA = 6 + 13 = 19.

