Câu hỏi:
Cho hình thoi ABCD có cạnh bằng a, O là tâm hình thoi, ^BAD=120°. Tính |→AD−→OC|
Trả lời:
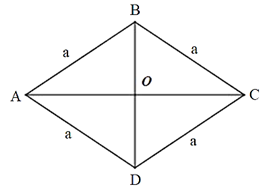
|→AD−→OC|=|→BC−→OC|=|→BO|=BO (vì AD = BC)
Lại có: Tam giác ABD cân tại A vì AB = AD nên AO là đường phân giác
Suy ra: ^BAO=12^BAD=60°
Xét tam giác AOB vuông tại O có: cos^BAO=cos60°=12=OBAB=OBa⇒OB=a2
Vậy |→AD−→OC|=a2
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm giao điểm I của AM và (SBD).
b) Tìm giao điểm P của SD và (ABM). Chứng minh rằng P là trung điểm của SD.
c) Gọi N là điểm tùy ý trên cạnh AB. Tìm giao điểm K của MN và (SBD).
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K, J lần lượt là trọng tâm tam giác ABC và tam giác SBC. Xác định thiết diện hình chóp cắt bởi mặt phẳng chứa KI và song song AD.
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.
Câu 4:
Câu 6:
Cho hình thoi ABCD, O là giao điểm hai đường chéo. Vẽ đường thẳng qua B song song AC, vẽ đường thẳng qua C song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì? Vì sao?
b) Chứng minh: AB = OK.
c) Tìm điều kiện của tứ giác ABCD để tứ giác OBKC là hình vuông.
Câu 7:
Cho hình thoi ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh MNPQ là hình chữ nhật.
Câu 8:
Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm giao tuyến của (GMN) và (ACD).
