Cho hình vuông ABCD cạnh a. Lấy M thuộc AB, N thuộc AD sao
Câu hỏi:
Cho hình vuông ABCD cạnh a. Lấy M thuộc AB, N thuộc AD sao cho AM + AN + MN = 2a. Chứng minh \(\widehat {MCN} = 45^\circ \).
Trả lời:
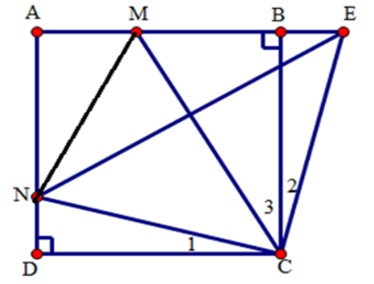
Vẽ tia Cx vuông góc với CN tại C, cắt AB tại E.
\(\widehat {{C_1}} + \widehat {MCN} + \widehat {{C_3}} = 90^\circ \)
\(\widehat {{C_2}} + \widehat {MCN} + \widehat {{C_3}} = 90^\circ \)
Suy ra: \(\widehat {{C_1}} = \widehat {{C_2}}\)
Xét tam giác CDN và tam giác CBE có:
\(\widehat {{C_1}} = \widehat {{C_2}}\)
CD = CB
\[\widehat {CDN} = \widehat {CBE} = 90^\circ \]
⇒ ∆CDN = ∆CBE (c.g.c)
⇒ CN = CE; DN = BE
Xét: AM + AN + ME
= AM + AN + MB + BE
= AM + AN + MB + ND (vì BE = ND, chứng minh trên)
= AM + MB + AN + ND
= AB + AD = 2a
Suy ra: AM + AN + ME = AM + AN + MN = 2a
Vậy MN = ME
Xét tam giác CMN và tam giác CME có:
CN = CE
Chung CM
MN = ME
⇒ ∆CMN = ∆CME (c.c.c)
⇒ \(\widehat {MCN} = \widehat {ECM}\)
Mà \(\widehat {MCN} + \widehat {ECM} = 90^\circ \)(do CE vuông góc CN)
Vậy \(\widehat {MCN} = 45^\circ \).

