Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến. Chứng minh: a. Tam giác ADE cân tại A. b. ∆ABD = ∆ACE. c. BCDE là hình thang cân.
Câu hỏi:
Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến. Chứng minh:
a. Tam giác ADE cân tại A.
b. ∆ABD = ∆ACE.
c. BCDE là hình thang cân.
Trả lời:
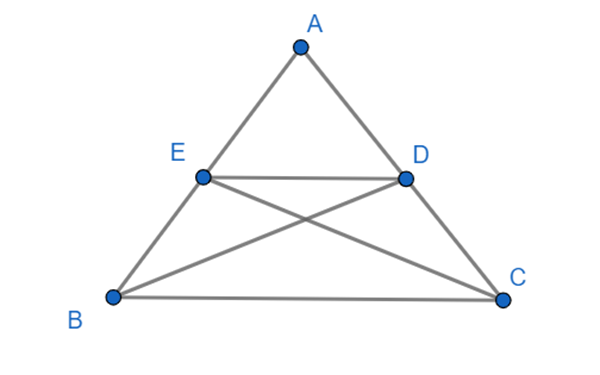
a. BD và CE là 2 đường trung tuyến.
⇒ EA = EB, DA = DC
Có ΔABC cân tại A ⇒ AB=AC
⇒ AE =AD
⇒ ΔAED cân tại A
b. Xét ΔABD và ΔACE có:
chung
AB = AC (GT)
AD = AE (chứng minh trên)
⇒ ΔABD = ΔACE (c.g.c)
c. EA = EB, DA=DC
⇒ ED là đường trung bình của ΔABC
⇒ ED //BC
⇒ tứ giác BCDE là hình thang
Lại có: ΔABD = ΔACE ⇒ BD = CE (Hai cạnh tương ứng)
⇒ BCDE là hình thang cân.

