Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD a) Chứng minh rằng AF // CE. b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.
Câu hỏi:
Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD
a) Chứng minh rằng AF // CE.
b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.
Trả lời:
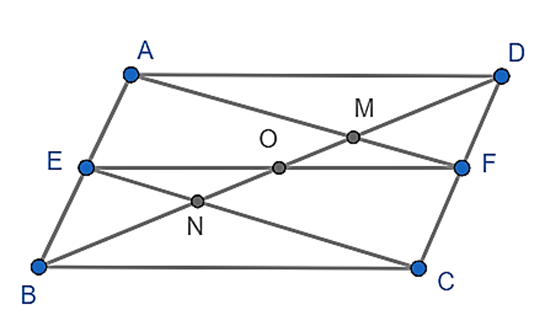
a) Ta có: AB // CD và AB = CD vì ABCD là hình bình hành
Nên AE // CF và AE = CF =
Suy ra: AECF là hình bình hành
Vậy AF // CE
b) Xét ΔAEM có E là trung điểm của AB
EN // AM
Do đó N là trung điểm của BM
⇒ BN = NM (1)
Xét ΔDNC có F là trung điểm của DC
FM // NC
Do đó: M là trung điểm của DN
⇒ DM = MN (2)
Từ (1) và (2) suy ra DM = MN = NB.