Cho tam giác ABC. Chứng minh có cosa/2.cosb/2.cosc/2 = sina/2.sinb/2.cosc/2 + sina/2.cosc/2.sinc/2 + cosa/2.sinb/2.sinc/2 =1/2

Câu hỏi:

Cho tam giác ABC. Chứng minh

$\cos \frac{A}{2} . \cos \frac{B}{2} . \cos \frac{C}{2} = \sin \frac{A}{2} . \sin \frac{B}{2} . \cos \frac{C}{2} + \sin \frac{A}{2} . \cos \frac{B}{2} . \sin \frac{C}{2} + \cos \frac{A}{2} . \sin \frac{B}{2} . \sin \frac{C}{2}$

Trả lời:

Ta có: $\frac{A + B + C}{2} = \frac{180 °}{2} = 90 ° \Rightarrow \cos (\frac{A}{2} + \frac{B}{2} + \frac{C}{2}) = \cos (90 °) = 0$

⇔ $\cos [(\frac{A}{2} + \frac{B}{2}) + \frac{C}{2}] = 0$

⇔ $\cos (\frac{A}{2} + \frac{B}{2}) . \cos \frac{C}{2} - \sin (\frac{A}{2} + \frac{B}{2}) . \sin \frac{C}{2} = 0$

⇔ $(\cos \frac{A}{2} . \cos \frac{B}{2} + \sin \frac{A}{2} . \sin \frac{B}{2}) . \cos \frac{C}{2} - (\sin \frac{A}{2} . \cos \frac{B}{2} + \cos \frac{A}{2} . \sin \frac{B}{2}) . \sin \frac{C}{2} = 0$

⇔ $\cos \frac{A}{2} . \cos \frac{B}{2} . \cos \frac{C}{2} - \sin \frac{A}{2} . \sin \frac{B}{2} . \cos \frac{C}{2} - \sin \frac{A}{2} . \cos \frac{B}{2} . \sin \frac{C}{2} - \cos \frac{A}{2} . \sin \frac{B}{2} . \sin \frac{C}{2} = 0$

⇔ $\cos \frac{A}{2} . \cos \frac{B}{2} . \cos \frac{C}{2} = \sin \frac{A}{2} . \sin \frac{B}{2} . \cos \frac{C}{2} + \sin \frac{A}{2} . \cos \frac{B}{2} . \sin \frac{C}{2} + \cos \frac{A}{2} . \sin \frac{B}{2} . \sin \frac{C}{2}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:

a) $\overset{⏜}{A P} = \overset{⏜}{B N}$

b) Tứ giác OKME là hình chữ nhật.

c) P, O, N thẳng hàng và KE // PN.

Xem lời giải »

Câu 2:

Cho đa thức R(x) = x² – 2x. Tính giá trị biểu thức $S = \frac{1}{R (3)} + \frac{1}{R (4)} + ... + \frac{1}{R (2022)} + \frac{1}{R (2023)}$

Xem lời giải »

Câu 3:

Rút gọn biểu thức: (4x – 1)³ - (4x − 3)(16x² + 3).

Xem lời giải »

Câu 4:

Cho tam giác ABC. Hai điểm M và N di chuyển sao cho $\vec{M N} = 2 \vec{M A} - \vec{M B} + \vec{M C}$ . Chứng minh MN luôn đi qua một điểm cố định.

Xem lời giải »

Câu 5:

Cho hình vuông ABCD cạnh a, M bất kì.

Tính độ dài của

$\vec{M A} + \vec{M B} + \vec{M C} - 3 \vec{M D}$

Xem lời giải »

Câu 6:

Tìm x để 50 chia hết cho x + 1.

Xem lời giải »

Câu 7:

Tìm x, y, z biết: $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ và x – y + z = –4.

Xem lời giải »

Câu 8:

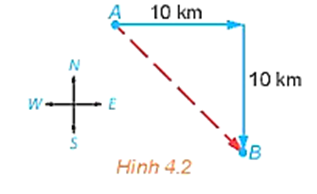
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải dài bao nhiêu kilômét?

Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (ảnh 1)

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho tam giác ABC. Chứng minh có cosa/2.cosb/2.cosc/2 = sina/2.sinb/2.cosc/2 + sina/2.cosc/2.sinc/2 + cosa/2.sinb/2.sinc/2 =1/2

Xem thêm bài tập Toán có lời giải hay khác: