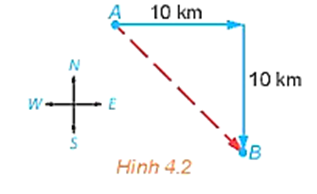
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng
Câu hỏi:
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải dài bao nhiêu kilômét?
Trả lời:
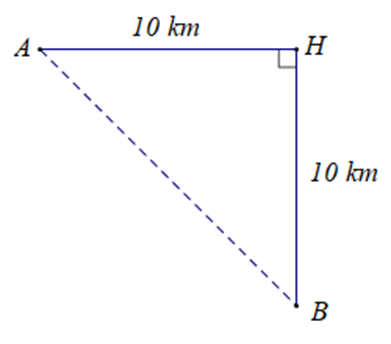
Ta có hình vẽ sau:
Vì góc giữa hướng đông và hướng nam là bằng 90 độ nên
do đó tam giác AHB vuông tại H.
Xét ΔAHB vuông tại H, áp dụng định lí Py – ta – go ta có: AB2 = AH2 + BH2
Thay số: AB2 = 102 + 10 = 100 + 100 = 200
⇔
ΔAHB vuông tại H, có AH = BH = 10 km nên ΔAHB cân tại H
Suy ra:
Do đó nếu đi từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B thì phải đi theo đường thẳng AB chính là hướng đông nam, tạo với hướng đông một góc 45°.
Vậy nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng đông nam, tạo với hướng đông một góc 45° và đi quãng đường dài
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a)
b) Tứ giác OKME là hình chữ nhật.
c) P, O, N thẳng hàng và KE // PN.
Xem lời giải »
Câu 2:
Cho đa thức R(x) = x2 – 2x. Tính giá trị biểu thức
Xem lời giải »
Câu 3:
Rút gọn biểu thức: (4x – 1)3 - (4x − 3)(16x2 + 3).
Xem lời giải »
Câu 4:
Cho tam giác ABC. Hai điểm M và N di chuyển sao cho . Chứng minh MN luôn đi qua một điểm cố định.
Xem lời giải »
Câu 5:
Tìm số tự nhiên n có 3 chữ số khác nhau biết rằng nếu xóa bất kì chữ số nào của nó ta cũng được một số là ước của n.
Xem lời giải »
Câu 6:
Tập giá trị của hàm số y = 2sin2x – sinx – 1 là đoạn [m; M]. Khi đó 8m – 3M bằng?
Xem lời giải »
Câu 7:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3 + 2x2 + (m − 3)x + m
có hai điểm cực trị và điểm M(9; −5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị.
Xem lời giải »
Câu 8:
Trên mặt phẳng tọa độ Oxy cho đường thẳng d: y = (2m + 10)x - 4m - 1 và điểm A(-2;3). Tìm m để khoảng cách từ A đến đường thẳng lớn nhất.
Xem lời giải »