Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin A

Câu hỏi:

Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin $\hat{A}$

Trả lời:

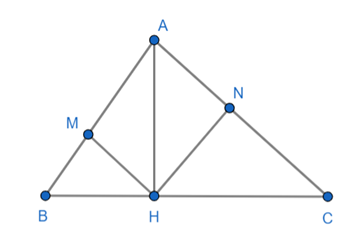
Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin A (ảnh 1)

Áp dụng hệ thức lượng trong tam giác vuông AHB, AHC có:

AH² = AM.AB

AH² = AN.AC

Suy ra: AM.AB = AN. AC

⇒ $\frac{A M}{A C} = \frac{A N}{A B}$

Xét tam giác AMN và tam giác ABC có:

$\frac{A M}{A C} = \frac{A N}{A B}$

$\hat{A}$ chung

⇒ ∆AMN ∽ ∆ABC (c.g.c)

⇒ $\frac{A M}{A C} = \frac{A N}{A B} = \frac{M N}{B C} \Rightarrow \frac{M N}{A N} = \frac{B C}{A B}$

⇒ $M N = \frac{B C . A N}{A B} = \frac{B C . A N . A C}{A B . A C} = \frac{B C . A H^{2}}{A B . A C}$ (1)

Lại có: $S_{A B C} = \frac{1}{2} . A H . B C = \frac{1}{2} . A B . A C . \sin \hat{A}$

Suy ra: $A H . B C = A B . A C . \sin \hat{A}$ (2)

Thay (2) vào (1) có:

M N = \frac{A H . A B . A C . \sin \hat{A}}{A B . A C} = A H . \sin \hat{A}

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính $\sin \hat{A C B}, \tan \hat{A C B}$

Xem lời giải »

Câu 2:

Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, $\hat{B} = 60 °$ . Bán kính đường tròn nội tiếp tam giác ABC là $r = \frac{2}{\sqrt{3}}$ cm. Tính đường cao AH của tam giác ABC.

Xem lời giải »

Câu 3:

Cho C = 5 + 5² + … + 5²⁰. Chứng minh rằng C chia hết cho 5, 6, 13.

Xem lời giải »

Câu 4:

Cho x + y = 12 và xy = 32. Tính x⁴ + y⁴.

Xem lời giải »

Câu 5:

Tìm x biết 18 chia hết cho x và x > 3.

Xem lời giải »

Câu 6:

Số nghiệm của phương trình

\sin (x + \frac{π}{4}) = 1

với π ≤ x ≤ 5π?

Xem lời giải »

Câu 7:

Với x > 9. Tìm GTNN của biểu thức

P = \frac{x}{\sqrt{x} - 3}

Xem lời giải »

Câu 8:

Một cột đèn có bóng trên mặt đất dài 8,5m . Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 38°. Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân).

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin A

Xem thêm bài tập Toán có lời giải hay khác: