Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác
Câu hỏi:
Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.
Trả lời:
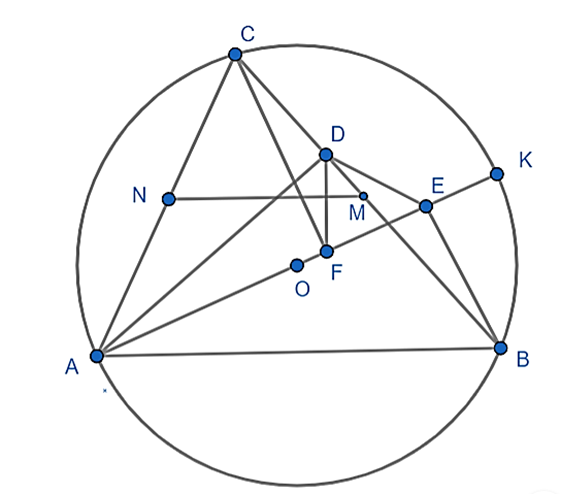
Xét ADFC có: \(\widehat {ADC} = \widehat {AFC} = 90^\circ \)(Vì AD ⊥ BC và CF ⊥ AK)
Suy ra: ADFC nội tiếp vì 2 góc cùng nhìn AC dưới 1 góc 90° không đổi.
⇒ \(\widehat {DFA} = \widehat {DCA}\)(cùng chắn cung AD) hay \(\widehat {DFA} = \widehat {BCA}\)
Mà \(\widehat {BKA} = \widehat {BCA}\)(góc nội tiếp)
Suy ra: \(\widehat {DFA} = \widehat {BKA}\)
Mà 2 góc \(\widehat {DFA};\widehat {BKA}\)ở vị trí đồng bị nên DF // BK
Mà BK ⊥ AB nên DF ⊥ AB
Mặt khác MN // AB (MN là đường trung bình của tam giác ABC)
Suy ra: MN ⊥ DF (đpcm).
Lại có: MN ⊥ DF
⇒ EM ⊥ DF
AK là đường kính, BC là đây cung (1)
⇒ AK ⊥ BC hay DM ⊥ DF (2)
Từ (1) và (2) suy ra: M là tâm đường tròn ngoại tiếp tam giác DEF.

