Cho tam giác ABC vuông cân tại A có BC = a căn bậc hai 2. Tính vecto CA . vecto CB
Câu hỏi:
Cho tam giác ABC vuông cân tại A có \(BC = a\sqrt 2 \). Tính \(\overrightarrow {CA} .\overrightarrow {CB} \).
A. a2
B. a
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \[{\rm{a}}\sqrt 2 \].
Trả lời:
Đáp án đúng là: A
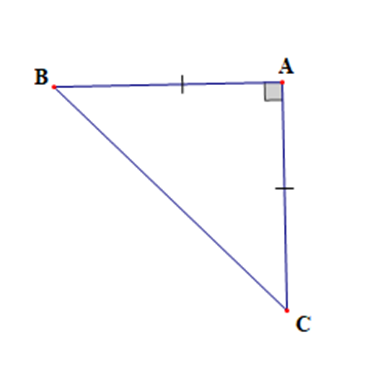
Vì tam giác ABC vuông cân tại A nên AB = AC và \(AB = AC = \sqrt {\frac{{B{C^2}}}{2}} = \sqrt {\frac{{2{{\rm{a}}^2}}}{2}} = a\)
Ta có : \(\overrightarrow {CA} .\overrightarrow {CB} = CA.CB.\cos 45^\circ = {\rm{ a}}{\rm{.a}}{\rm{. }}\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}\)
Vậy ta chọn đáp án A.

