Cho tam giác ABC vuông cân tại A và điểm M thuộc cạnh BC. Chứng minh MB^2 + MC^2 = 2MA^2.
Câu hỏi:
Cho tam giác ABC vuông cân tại A và điểm M thuộc cạnh BC. Chứng minh MB2 + MC2 = 2MA2.
Trả lời:
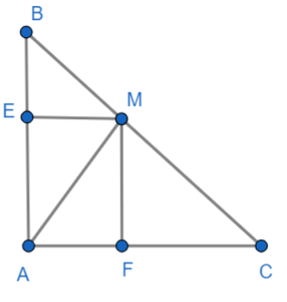
Từ M kẻ ME vuông góc với AB, MF vuông góc với AC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM, FMC, AEF ta có:
BM2 = EM2 + BE2 = 2.ME2 ; MC2 = 2.FM2
⇒ BM2 + MC2 = 2.(ME2 + MF2) (1)
Mà AM2 = EF2 = ME2 + MF2 (2)
Từ (1),(2) ta được MB2 + MC2 = 2MA2.


