cho tam giác ABC vuông tại A, BC = 4cm. Đường cao AH, kẻ HI vuông góc AB, HK vuông góc AC. Tìm giá trị lớn nhất của diện tích tứ giác AIHK.
Câu hỏi:
cho tam giác ABC vuông tại A, BC = 4cm. Đường cao AH, kẻ HI vuông góc AB, HK vuông góc AC. Tìm giá trị lớn nhất của diện tích tứ giác AIHK.
Trả lời:
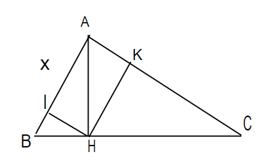
Đặt AB = x
Dễ chứng minh tam giác HBA và tam giác ABC đồng dạng (g.g)
⇒ AB2 =BH.BC
⇒ x2 = 4BH
Hay BH =
Lại có: AB2= BH2+ AH2
⇒ AH2 =
Suy ra:
Dấu “=” khi x2 = 16 – x2 hay x = AB = ; HI = HK thì tam giác ABC vuông cân tại A.


