Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH

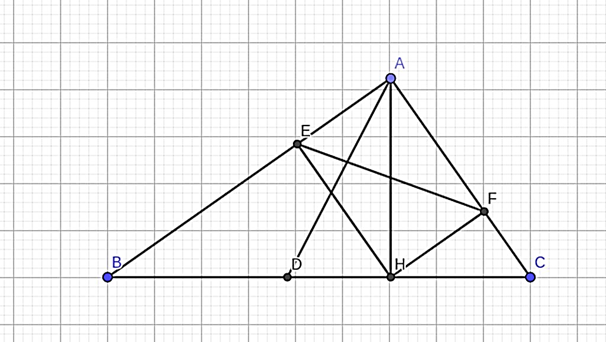
a) Ta có tam giác ABC vuông tại A, AH ⊥ BC

Nên: AH² = BH.CH = 18.8 = 144

⇒ AH = 12cm.

AC = \(\sqrt {A{H^2} + H{C^2}} = 4\sqrt {13} \)

b) Vì AD là phân giác \(\widehat {BAH}\) ⇒ \(\widehat {BAD} = \widehat {DAH}\)

\(\widehat {HAC} = 90^\circ - \widehat {HAB} = \widehat {ABH} = \widehat {ABD}\)

⇒ \(\widehat {CDA} = \widehat {DAB} + \widehat {DBA} = \widehat {DAH} + \widehat {CAH} = \widehat {CAD}\)

Suy ra: tam giác CAD cân tại C ⇒ CA = CD

Vì AD là phân giác \(\widehat {BAH}\) ⇒ \(\frac{{DH}}{{DB}} = \frac{{AH}}{{AB}} = \sin B = \frac{{AC}}{{BC}}\)

⇒ HD.BC = BD.AC = DB.CD

c) Ta có: HE ⊥ AB, HF ⊥ AC, AB ⊥ AC

Nên AEHF là hình chữ nhật

⇒ AH = EF

⇒ \(\widehat {AEF} = \widehat {EAH} = \widehat {BAH} = 90^\circ - \widehat B = \widehat {ACB}\)

Mà \(\widehat {EAF} = \widehat {BAC}\)

⇒ ∆AFE ∼ ∆ABC (g.g)

⇒ \(\frac{{{S_{AFE}}}}{{{S_{ABC}}}} = {\left( {\frac{{EF}}{{BC}}} \right)^2} = \frac{{A{H^2}}}{{B{C^2}}}\)
Ta có: 1 – cos²B = sin²B

⇒ (1 – cos²B)sin²C = sin²Bsin²C = (sinBsinC)²

= \({\left( {\frac{{AC}}{{BC}}.\frac{{AB}}{{BC}}} \right)^2} = {\left( {\frac{{AB.AC}}{{B{C^2}}}} \right)^2} = {\left( {\frac{{AH.BC}}{{B{C^2}}}} \right)^2} = {\left( {\frac{{AH}}{{BC}}} \right)^2}\)

⇒ \[\frac{{{S_{AFE}}}}{{{S_{ABC}}}} = \left( {1--co{s^2}B} \right)si{n^2}C\]

⇒ _AEF = S_ABC.(1 – cos²B).sin²C.