Cho tam giác ABC vuông tại A (AB < AC) đường cao AH
Câu hỏi:
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH
1) Giả sử AB = 9cm, AC = 12cm. Tỉnh độ dài các đoạn thẳng BC, BH và AH.
2) Gọi M và N lần lượt là chân các đường vuông góc kẻ từ điểm H đến các đường
thằng AB và AC . Chứng minh AM.AB = AN.AC.
3) Đường thẳng đi qua điểm A và song song với đường MN cắt đường thẳng đi qua điểm C và song song với đường AH tại điểm K. Gọi I là giao điểm của AH và BK. Chứng minh ba điểm M, L, N là ba điểm thẳng hàng.
Trả lời:
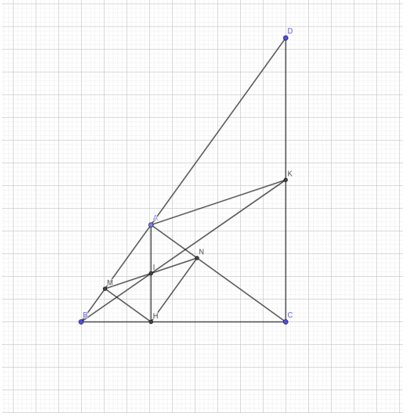
1)
ΔABC vuông tại A, AH ⊥ BC nên AH.BC = AB.AC
Suy ra:
2) Áp dụng hệ thức lượng trong tam giác vuông AHB, AHC có:
AH2 = AM.AB
AH2 = AN.AC
Suy ra: AM.AB = AN.AC
3) Gọi AB ∩ CK = D
Vì HM ⊥ AB, HN ⊥ AC, AB ⊥ AC
⇒ AMHN là hình chữ nhật
MN // AK, KC // AH
⇒
⇒ ΔKAC cân tại K
⇒ AK = KC
Ta có: AB ⊥ AC⇒ AD ⊥ AC
⇒
⇒ΔKAD cân tại K
⇒ AK = KD
⇒ KD = KC
Ta có: AH // CD (⊥BC)
⇒
⇒ IA = IH
⇒ I là trung điểm AH
Mà AMHN là hình chữ nhật
⇒ AH ∩ MN tại trung điểm mỗi đường
⇒ I là trung điểm MN
⇒ M, I, N thẳng hàng


