Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, CH = 12cm. Tính AH?
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, CH = 12cm. Tính AH?
Trả lời:
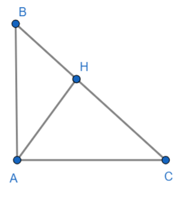
Áp dụng hệ thức lượng trong tam giác vuông ta có:
BH.HC = AH2
Suy ra: AH = .


