Cho tam giác ABC vuông tại A, đường cao AH, vẽ HE vuông góc AB
Câu hỏi:
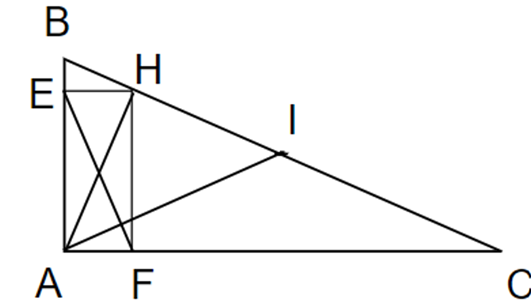
Cho tam giác ABC vuông tại A, đường cao AH, vẽ HE vuông góc AB, HF vuông góc AC. Gọi I là trung điểm BC.
a) Chứng minh EF = AH.
b) Chứng minh AI vuông góc EF.
c) Gọi M là trung điểm HB, N là trung điểm HC. Chứng minh EMNF là hình thang vuông.
Trả lời:
a) Ta có \(\widehat E = \widehat A = \widehat F = 90^\circ \) nên EAFH là hình chữ nhật
Suy ra EF = AH (hai đường chéo của một hình chữ nhật)
b) Tam giác ABC vuông tại A có trung tuyến AI
Suy ra AI = \(\frac{1}{2}BC\)= BI = IC
⇒ΔIAB cân tại I nên \(\widehat {IAB} = \widehat {IBA}\)(1)
EAFH là hình chữ nhật suy ra EF = AH
Gọi O là giao điểm EF và AH
Suy ra EO = OF = OA = OH hay tam giác EOA cân tại O
Nên \(\widehat {OEA} = \widehat {OAE}\) (2)
Mà \(\widehat {IBA} + \widehat {OAE} = 90^\circ \)
Từ (1), (2) và (3) suy ra \(\widehat {IAE} + \widehat {OEA} = 90^\circ \) hay AI ⊥ EF
c) Xét tam giác EBH vuông tại E có EM là trung tuyến ứng với cạnh huyền
⇒ EM = MB = \(\frac{1}{2}BH\)
⇒ ΔEMB cân tại M
⇒ \(\widehat {MBE} = \widehat {MEB}\)
Mà \(\widehat {MBE} + \widehat {ACB} = 90^\circ \)(do tam giác ABC vuông tại A)
\(\widehat {ACB} = \widehat {AEO}\)(=\(\widehat {AHO}\))
⇒ \(\widehat {BEM} + \widehat {AEO} = 90^\circ \)
⇒ \(\widehat {MEF} = 180^\circ - 90^\circ = 90^\circ \)
Suy ra: ME vuông góc với EF tại E
Chứng minh tương tự: NF vuông góc với EF tại F
Xét tứ giác MEFN có ME ⊥ EF; NF ⊥ EF
Suy ra: ME // NF
⇒ MENF là hình thang
Đồng thời \(\widehat {MEF} = \widehat {EFN} = 90^\circ \)
⇒ MEFN là hình thang vuông tại E và F.

