Cho hình vuông ABCD. Lấy M thuộc AB và N thuộc BC sao cho
Câu hỏi:
Cho hình vuông ABCD. Lấy M thuộc AB và N thuộc BC sao cho BN = BM. Gọi H là hình chiếu vuông góc của B lên CM. Chứng minh rằng \(\widehat {DHN}\) = 90°.
Trả lời:
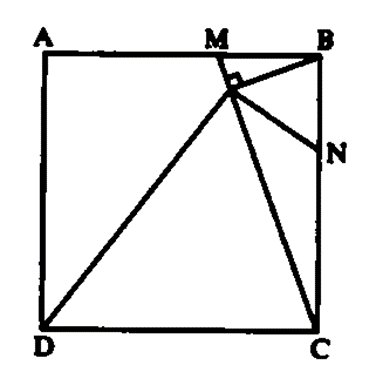
Đặt a là độ dài các cạnh của hình vuông, α = \(\widehat {MBH} = \widehat {BCH}\)
Ta có: \[\overrightarrow {HN} .\overrightarrow {HD} = \left( {\overrightarrow {HB} + \overrightarrow {BN} } \right)\left( {\overrightarrow {HC} + \overrightarrow {CD} } \right) = \overrightarrow {HB} .\overrightarrow {CD} + \overrightarrow {BN} .\overrightarrow {HC} \] (vì \(\overrightarrow {HB} \bot \overrightarrow {HC} ;\overrightarrow {BN} \bot \overrightarrow {CD} \))
= \[\overrightarrow {HB} .\overrightarrow {BA} + \overrightarrow {BN} .\overrightarrow {HC} \]
= –HB.a.cosφ + BN.HC.cosφ
= –MB.a.cos2φ + NB.a.cos2φ
= 0 (vì MB = NB)
Suy ra: \[\overrightarrow {HN} \bot \overrightarrow {HD} \]
Vậy \(\widehat {DHN}\) = 90°.

