Cho tam giác đều ABC cạnh 2a, G là trọng tâm. Khi đó độ dài vecto AB - vecto GC bằng?
Câu hỏi:
Cho tam giác đều ABC cạnh 2a, G là trọng tâm. Khi đó độ dài bằng?
Trả lời:
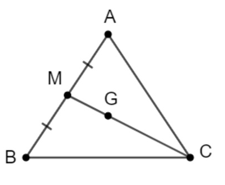
Gọi M là trung điểm AB
.
Câu hỏi:
Cho tam giác đều ABC cạnh 2a, G là trọng tâm. Khi đó độ dài bằng?
Trả lời:

Gọi M là trung điểm AB
.
Câu 1:
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho . Điểm M di động nằm trên BC sao cho . Tìm x sao cho độ dài của đạt giá trị nhỏ nhất.
Câu 4:
Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = , diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?
Câu 5:
Tam giác ABC đều cạnh a, dựng hình vuông BCMN. Gọi G là trọng tâm tam giác ABC. Tính theo a độ dài vectơ .
