Cho tứ diện ABCD có M nằm trên cạnh AB, N nằm trên cạnh AD thoả MB = 2MA, AN = 2ND. Gọi P là điểm thuộc miền trong của tam giác BCD.
Câu hỏi:
Cho tứ diện ABCD có M nằm trên cạnh AB, N nằm trên cạnh AD thoả MB = 2MA, AN = 2ND. Gọi P là điểm thuộc miền trong của tam giác BCD. Tìm giao tuyến của (MNP) và (ABC).
Trả lời:
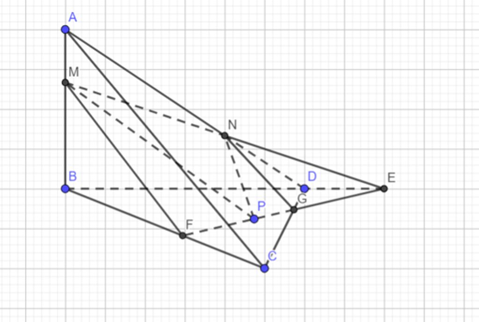
Dựng hình theo hình vẽ.
Ta có: MB = 2MA, AN = 2ND nên:
Nên MN không song song với BD
Gọi MN ∩ BD = E, EP ∩ BC = F
Suy ra: (MNP) ∩ (ABC) = MF.

