Cho x, y là các số thực thỏa mãn log 4 (x+y)+log 4 (x-y0 lớn hơn bằng 1

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho x, y là các số thực thỏa mãn $\log_{4} (x + y) + \log_{4} (x - y) \geq 1$ . Tìm giá trị nhỏ nhất $P_{m i n}$ của biểu thức $P = 2 x - y$

A. $P_{m i n} = 4$

B. $P_{m i n} = - 4$

C. $P_{m i n} = 2 \sqrt{3}$

D. $P_{m i n} = \frac{10 \sqrt{3}}{3}$

Trả lời:

Điều kiện: x+y>0, x-y>0

$\log_{4} (x + y) + \log_{4} (x - y) \geq 1 \Leftrightarrow \log_{4} (x^{2} - y^{2}) \geq 1 \Leftrightarrow x^{2} - y^{2} \geq 4$

Ta có:

$P = 2 x - y = \frac{x + y + 3 (x - y)}{2} \geq \sqrt{(x + y) . 3 (x - y)} = \sqrt{3 (x^{2} - y^{2})} \geq \sqrt{3.4} = 2 \sqrt{3}$

Dấu bằng xảy ra khi:

$\{\begin{cases} x + y = 3 (x - y) \\ x^{2} - y^{2} = 4 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 3 (x - y) \\ 3 {(x - y)}^{2} = 4 \end{cases} \Leftrightarrow \{\begin{cases} x - y = \frac{2}{\sqrt{3}} \\ x + y = 2 \sqrt{3} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{\sqrt{3}} + \sqrt{3} \\ y = - \frac{1}{\sqrt{3}} + \sqrt{3} \end{cases}$

Vậy $P_{m i n} = 2 \sqrt{3}$

Đáp án cần chọn là: C.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số $y = \log_{\frac{π}{4}} x$ . Khẳng định nào sau đây sai?

Xem lời giải »

Câu 2:

Đồ thị hàm số dưới đây là của hàm số nào?

Xem lời giải »

Câu 3:

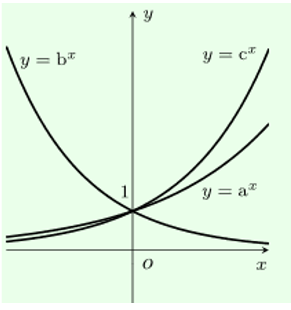
Cho các đồ thị hàm số $y = a^{x}, y = b^{x}, y = c^{x} (0 < a, b, c \neq 1)$ . Chọn khẳng định đúng:

Xem lời giải »

Câu 4:

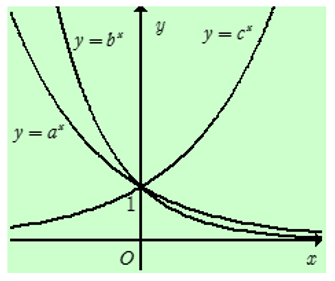
Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số $y = a^{x}, y = b^{x}, y = c^{x}$ . Khẳng định nào sau đây là đúng?

Xem lời giải »

Câu 5:

Cho a là một số thực dương khác 1 và các mệnh đề sau:

Hàm số $y = {(- 5)}^{x}$ là hàm số mũ

Nếu $π^{α} < π^{2 α}$ thì $α < 1$

Hàm số $y = a^{x}$ có tập xác định là R

Hàm số $y = a^{x}$ có tập giá trị là $(0; + \infty)$

Hỏi có bao nhiêu mệnh đề đúng?

Xem lời giải »

Câu 6:

Hàm số nào sau đây nghịch biến trên $(- \infty; + \infty)$

Xem lời giải »

Câu 7:

Cho hàm số $y = 2^{x^{2} - 3 x}$ có đạo hàm là:

Xem lời giải »

Câu 8:

Đạo hàm của hàm số $y = 2^{\sin x}$ là:

Xem lời giải »

❮ Bài trước Bài sau ❯

2018 © All Rights Reserved.

DMCA.com Protection Status