Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Câu hỏi:

Trả lời:

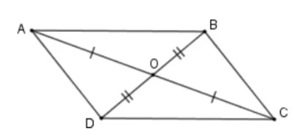
Gọi O là giao điểm của hai đường chéo.

Theo giả thiết ta có: OA = OC; OB = OD

Xét tam giác AOD và tam giác BOC có:

OA = OC

$\hat{A O D} = \hat{B O C}$ (đối đỉnh)

OB = OD

⇒ ∆AOD = ∆BOC (c.g.c)

Suy ra: AD = BC và $\hat{A D O} = \hat{B C O}$

Mà $\hat{A D O}, \hat{B C O}$ ở vị trí so le trong nên AD // BC
Suy ra: ABCD là hình bình hành vì AD = BC và AD // BC.

Câu 1:

Cho x + y = 15. Tìm min, max $B = \sqrt{x - 4} + \sqrt{y - 3}$

Câu 2:

Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.

Câu 3:

Cho x, y, z thỏa mãn đk x + y + z = a. Tìm GTNN của $P = (1 + \frac{a}{x}) (1 + \frac{a}{y}) (1 + \frac{a}{z})$

Câu 4:

Cho x + 3y – 4 = 0, tính x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

Câu 5:

Chứng minh n + 1 và 2n + 3 là hai số nguyên tố cùng nhau.

Câu 6:

Chứng minh rằng nếu 5(m + n)² + mn ⋮ 441 thì mn ⋮ 441 (m, n ∈ ℤ)

Câu 7:

Cho $\frac{a}{b} = \frac{c}{d}$ với a, b, c, d khác 0. Chứng minh $\frac{a}{a - b} = \frac{c}{c - d}$

Câu 8:

Cho tứ giác ABCD. Chứng minh $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$

Các dạng bài tập Toán lớp 12