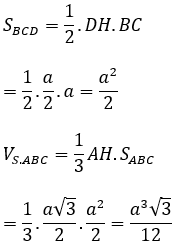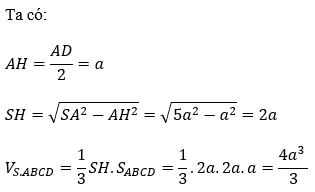Tổng hợp công thức tính thể tích đa diện cực hay - Toán lớp 12
Tổng hợp công thức tính thể tích đa diện cực hay
Tài liệu Tổng hợp công thức tính thể tích đa diện cực hay Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về tính thể tích đa diện từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

1. Công thức tính thể tích Tứ diện đều
1. Tứ diện đều thuộc loại {3; 3}
2. Tất cả các cạnh bằng nhau, tất cả các mặt là tam giác đều.
3. Đường cao:
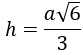
4. Thể tích:
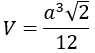
5. Diện tích toàn phần:
Stoàn phần = 4Sđáy= a2√3
2. Công thức tính thể tích hình Lập phương
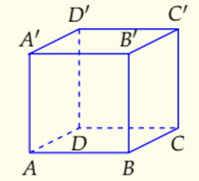
1. Thể tích khối lập phương V = a3
2. Diện tích toàn phần Stp = 6a2
3. Độ dài đường chéo: a√3
3. Công thức tính thể tích hình Chóp tứ giác đều
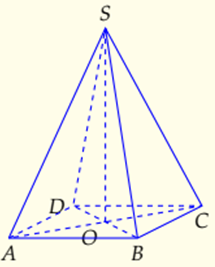
1. Chóp tứ giác đều S.ABCD là đa diện đều thuộc loại hình chóp có đáy là hình vuông và SO⊥(ABCD)
2. Các cạnh đáy bằng nhau và các cạnh bên bằng nhau, các mặt bên là những tam giác cân.
3. Không có tâm đối xứng.
4. Có 1 trục đối xứng.
5. Có 4 mặt phẳng đối xứng.
6. Thể tích:
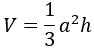
7. Diện tích toàn phần:
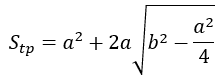
4. Công thức tính thể tích hình Lăng trụ tam giác đều
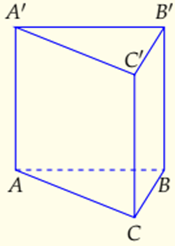
1. Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.
2. Các cạnh đáy bằng nhau và các cạnh bên bằng nhau, các mặt bên là những hình chữ nhật.
3. Không có tâm đối xứng và trục đối xứng.
4. Có 4 mặt phẳng đối xứng.
5. Thể tích:
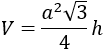
6. Diện tích toàn phần:
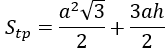
5. Công thức tính thể tích Khối hộp chữ nhật
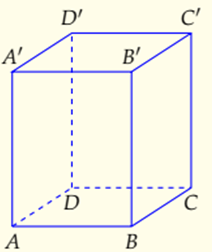
1. Hình hộp chữ nhật là lăng trụ đứng, có mặt đáy là hình chữ nhật.
2. Tất cả các mặt đều là hình chữ nhật.
3. Không có tâm đối xứng.
4. Có 3 trục đối xứng.
5. Có 3 mặt phẳng đối xứng.
6. Thể tích khối hộp chữ nhật: V=abc
7. Diện tích toàn phần Stp = 2(ab+bc+ca)
8. Độ dài đường chéo 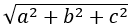
Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy
A. Phương pháp giải & Ví dụ
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là một đa giác đều và các cạnh bên bằng nhau.
2. Kết quả: Trong hình chóp đều:
+ Đường cao hình chóp qua tâm của đa giác đáy.
+ Các cạnh bên tạo với đáy các góc bằng nhau.
+ Cắt mặt bên tạo với đáy các góc bằng nhau.
Ví dụ minh họa
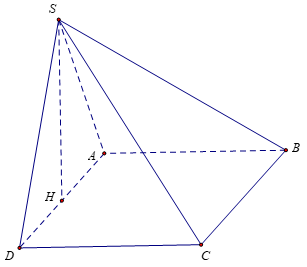
Bài 1: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5
Hướng dẫn:
Bài 2: Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB = 3a, AC = 6a. Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH = 2HB. Biết SC hợp với (ABC) một góc bằng 60º . Tính thể tích khối chóp S.ABC
Hướng dẫn:
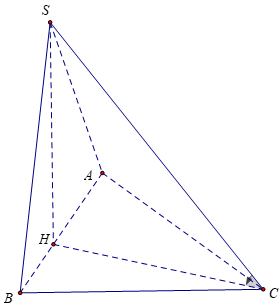
Tam giác ABC vuông tại B, AB = 3a, AC = 6a
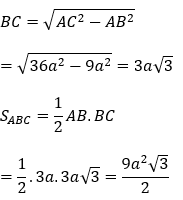
AH = 2HB; AB = 3a ⇒ HB = a
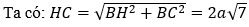
Có: SH⊥(ABCD) nên góc giữa SC và (ABC) là góc giữa SC và HC
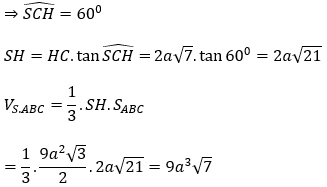
Tính thể tích khối chóp có mặt bên vuông góc với đáy
A. Phương pháp giải & Ví dụ
Để xác định đường cao hình chóp, ta vận dụng định lí sau:
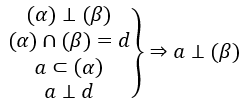
Ví dụ minh họa
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB=2a√3 và ∠(SBC)=30º. Tính thể tích khối chóp S.ABC
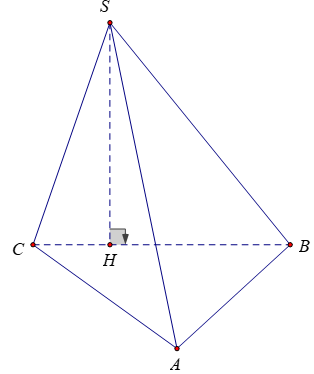
Kẻ SH vuông góc với BC
Xét tam giác SHB vuông tại H có:
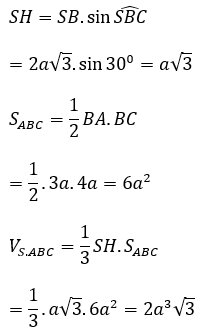
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt bên (SAB) là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD. Tính thể tích khối chóp S.ABCD
Gọi H là trung điểm của AB
∆SAB đều nên SH ⊥ AB
(SAB) ⊥ (ABCD) ⇒ SH ⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
Ta có: ∆SAB đều cạnh a nên SH = a√3/2
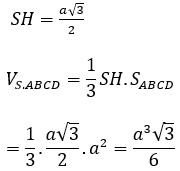
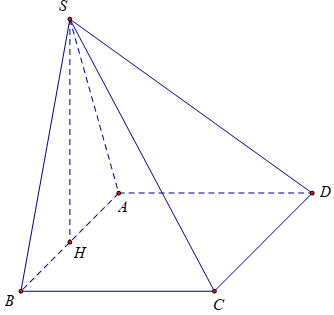
Bài 3: Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D. (ABC) ⊥ (BCD) và AD hợp với (BCD) một góc 60º, AD = a. Tính thể tích của tứ diện ABCD
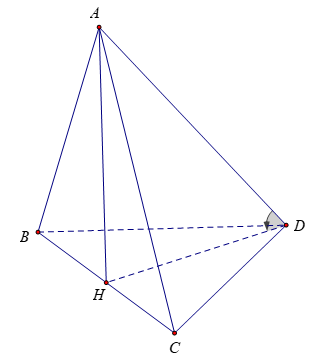
Gọi H là trung điểm của BC. Ta có tam giác ABC đều nên AH ⊥ BC
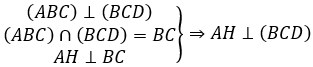
Ta có: HD là hình chiếu vuông góc của DA lên mặt phẳng (BCD)
Do đó, góc giữa HD và mặt phẳng (BCD) là góc giữa AD và DH
⇒ ∠(ADH) =60º
Xét tam giác AHD vuông tại H có:
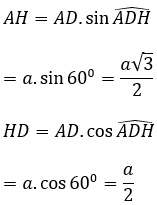
BCD là tam giác vuông cân tại D có DH là trung tuyến nên
BC=2DH=a