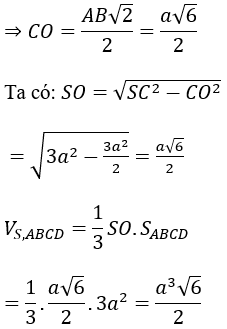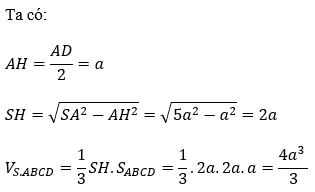Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy cực hay - Toán lớp 12
Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy cực hay
Với Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là một đa giác đều và các cạnh bên bằng nhau.
2. Kết quả: Trong hình chóp đều:
+ Đường cao hình chóp qua tâm của đa giác đáy.
+ Các cạnh bên tạo với đáy các góc bằng nhau.
+ Cắt mặt bên tạo với đáy các góc bằng nhau.
Ví dụ minh họa
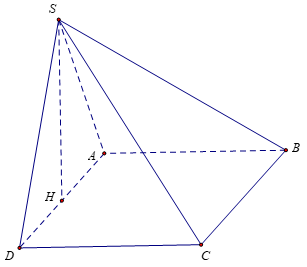
Bài 1: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5
Hướng dẫn:
Bài 2: Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB = 3a, AC = 6a. Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH = 2HB. Biết SC hợp với (ABC) một góc bằng 60º . Tính thể tích khối chóp S.ABC
Hướng dẫn:
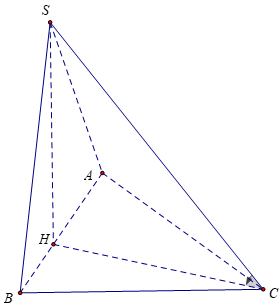
Tam giác ABC vuông tại B, AB = 3a, AC = 6a
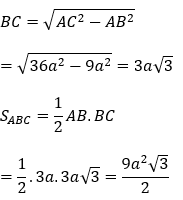
AH = 2HB; AB = 3a ⇒ HB = a
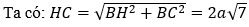
Có: SH⊥(ABCD) nên góc giữa SC và (ABC) là góc giữa SC và HC
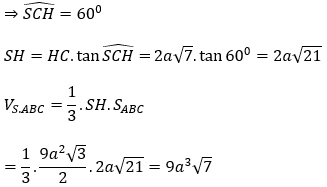
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, BC=a√3, H là trung điểm của cạnh AD. Biết hai mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt đáy, đường thẳng SD tạo với đáy một góc 60º . Tính thể tích của khối chóp theo a
Hướng dẫn:
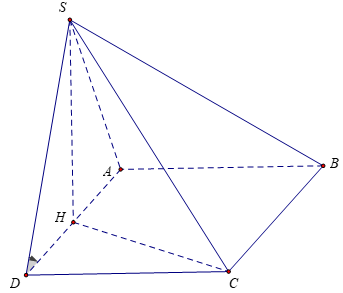
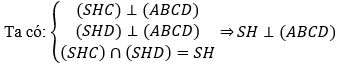
HD là hình chiếu vuông góc của SD lên mặt phẳng (ABCD). Do đó góc giữa đường thẳng SD và đáy là góc giữa HD và SD
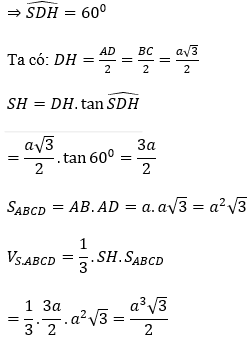
Bài 4: Cho khối chóp đều S.ABCD có cạnh đáy bằng a√3. Tính thể tích khối chóp S.ABCD biết góc giữa cạnh bên và mặt đáy bằng 60°.
Hướng dẫn:
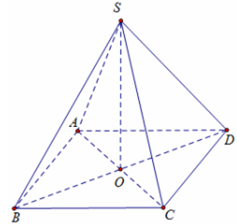
Gọi O là tâm của hình vuông ABCD khi đó SO⊥(ABCD)
suy ra góc SDO =(SD,(ABCD))=60º .
Lại có đáy ABCD là hình vuông cạnh a√3
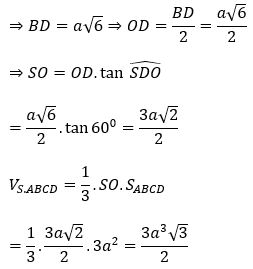
Bài 5: Cho hình chóp S.ABC có góc giữa SC và mặt đáy bằng 45º , đáy ABC là tam giác vuông tại A có AB = 2a, góc ABC =60º và hình chiếu của S lên mặt phẳng (ABC) là trung điểm của AB. Tính theo a thể tích của khối chóp S.ABC
Hướng dẫn:
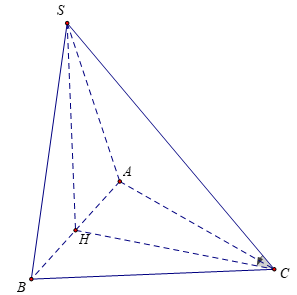
Gọi H là trung điểm của AB
Tam giác ABC vuông tại A có AB = 2a, góc ABC = 60º
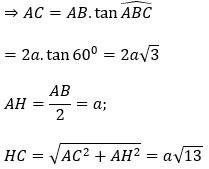
HC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD), do đó, góc giữa SC và (ABCD) là góc giữa HC và SC
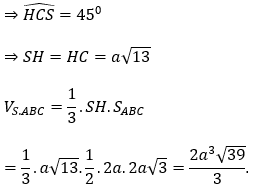
B. Bài tập vận dụng
Bài 1: Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 2a. Gọi H là trung điểm AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABCD biết tam giác SAB đều.
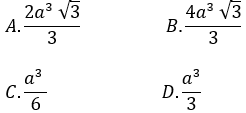
Lời giải:
Đáp án : B
Giải thích :
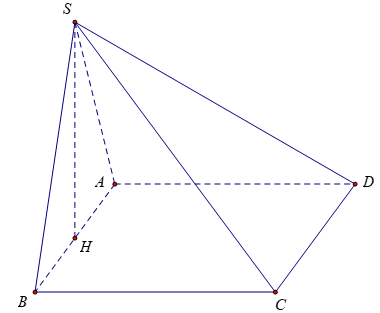
Tam giác SAB đều cạnh 2a nên SH=a√3
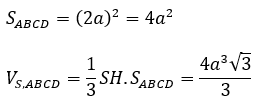
Bài 2: Cho khối chóp đều S.ABC có cạnh đáy bằng a. Tính thể tích khối chóp S.ABC biết cạnh bên bằng 2a.
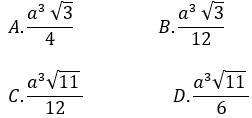
Lời giải:
Đáp án : C
Giải thích :
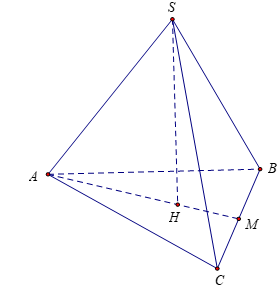
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ (ABC)
Gọi M là trung điểm của BC ta có
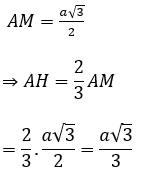
Lại có
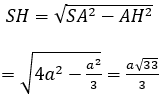
∆ABC đều cạnh a nên
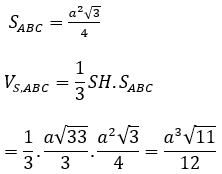
Bài 3: Cho khối chóp đều S.ABC có cạnh đáy bằng a. Tính thể tích khối chóp S.ABC biết góc giữa cạnh bên và mặt đáy bằng 45º.
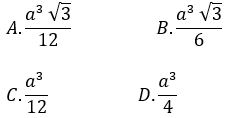
Lời giải:
Đáp án : C
Giải thích :
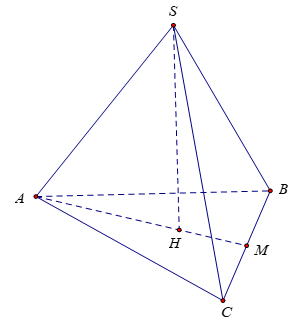
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ (ABC)
Gọi M là trung điểm của BC ta có
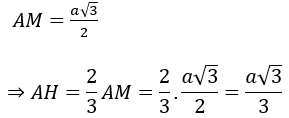
HA là hình chiếu vuông góc của SH lên mặt đáy (ABC)
Do đó, góc giữa cạnh bên SA và mặt đáy là góc giữa AH và SA
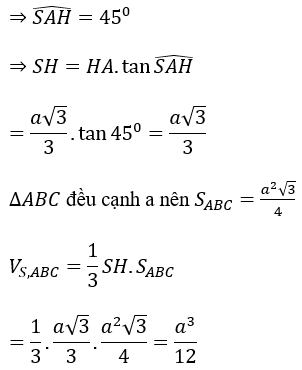
Bài 4: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Gọi H là trung điểm AB, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 60º
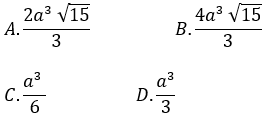
Lời giải:
Đáp án : B
Giải thích :
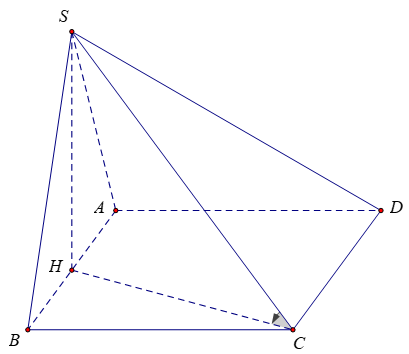
Ta có: HC là hình chiếu của SC trên mặt phẳng (ABCD), do đó góc giữa SC và (ABCD) là góc giữa SC và HC
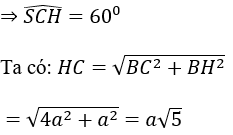
Xét tam giác SCH vuông có:
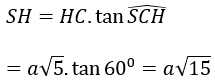
ABCD là hình vuông cạnh 2a n ên SABC = 4a2
Vậy thể tích khối chóp S.ABCD là:
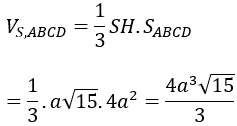
Bài 5: Cho khối chóp đều S.ABCD có cạnh đáy bằng 2a. Mặt bên hợp với đáy một góc 60º Tính thể tích khối chóp S.ABC
Lời giải:
Đáp án : D
Giải thích :
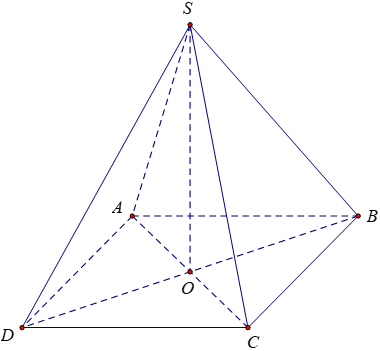
Gọi O là tâm của hình vuông ABCD khi đó SO ⊥ (ABCD)
Ta có: OA là hình chiếu vuông góc của SA lên mặt phẳng (ABCD)
Khi đó, góc giữa cạnh bên SA và mặt phẳng (ABCD) là góc giữa SA và OA
⇒ ∠(SAO) = 60º
Lại có: ABCD là hình vuông cạnh 2a, O là giao điểm của hai đường chéo
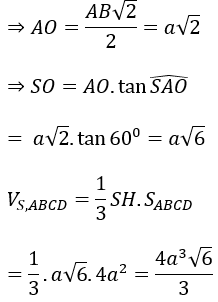
Bài 6: Cho khối chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2a. Hình chiếu của S trên mặt phẳng (ABCD) là trung điểm H thuộc đoạn AO. Góc giữa mặt phẳng (SCD) và (ABCD) bằng 60º. Tính thể tích khối chóp S.ABCD
Lời giải:
Đáp án : D
Giải thích :
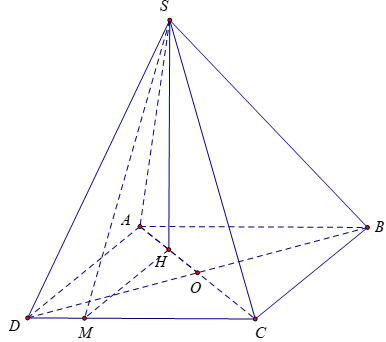
Gọi M là hình chiếu vuông góc của H lên CD.
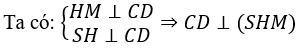
(SCD) ∩ (ABCD) = CD
Và mặt phẳng (SHM) cắt hai mặt phẳng (SCD) và (ABCD) lần lượt tại các giao tuyến SM và HM.
Do đó, góc giữa hai mặt phẳng (SCD) và (ABCD) là góc giữa SM và HM
⇒ ∠(SMH) = 60º
HM // AD nên ta có:
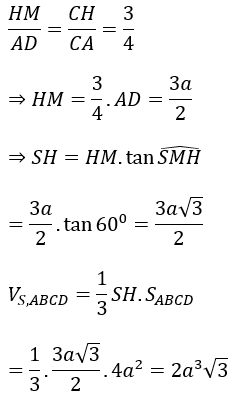
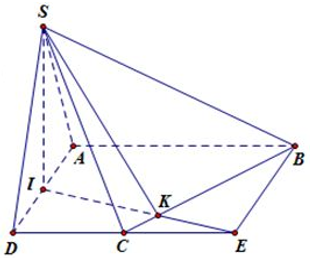
Bài 7: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB=AD=2a;CD=a. Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60º. Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
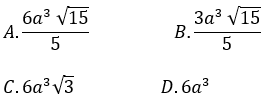
Lời giải:
Đáp án : B
Giải thích :
Lấy E là điểm đối xứng với D qua C, suy ra tứ giác ABED là hình vuông. Gọi K là giao điểm của IE và BC.
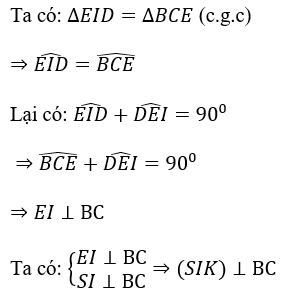
Mặt phẳng (SIK) vuông góc với BC là giao tuyến của (SBC) và (ABCD), đồng thời cắt 2 mặt phẳng này tại các giao tuyến SK và IK, suy ra

Ta có:
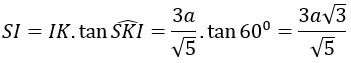
Đáy ABCD là hình thang vuông tại A và D; AB=AD=2a;CD=a nên
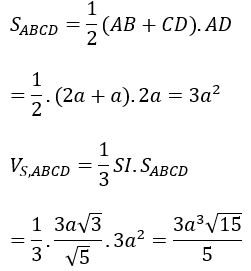
Bài 8: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Biết AD = 2BC = 2a và BD=a√5. Tính thể tích khối chóp S.ABCD biết rằng góc giữa SB và (ABCD) bằng 30º
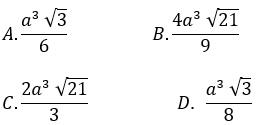
Lời giải:
Đáp án : A
Giải thích :
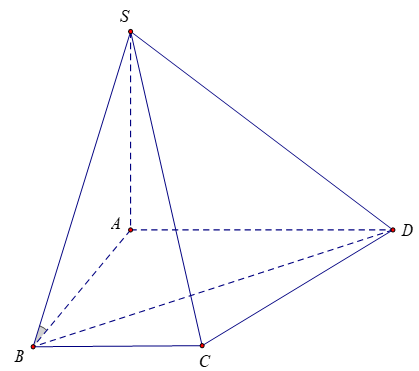
Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy; (SAB) ∩ (SAD) = SA
⇒ SA ⊥ (ABCD)
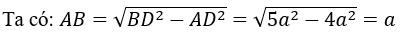
AB là hình chiếu vuông góc của SB lên mặt phẳng (ABCD) nên góc giữa SB và mặt đáy (ABCD) là góc giữa AB và SB
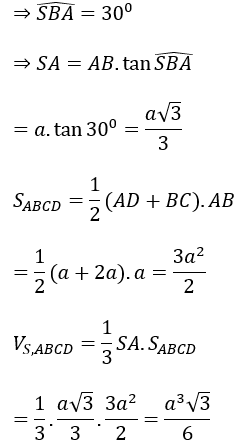
Bài 9: Cho khối chóp đều S.ABC có cạnh đáy bằng a√3. Tính thể tích khối chóp S.ABC biết mặt bên là tam giác vuông cân.
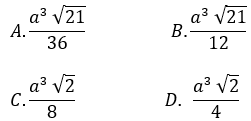
Lời giải:
Đáp án : C
Giải thích :
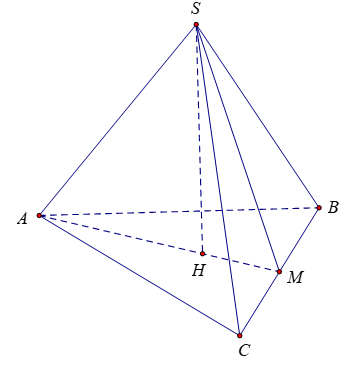
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ (ABC)
Gọi M là trung điểm của BC ta có AM = 3a/2

∆ABC đều cạnh a√3 nên SABC = (3a2)/4
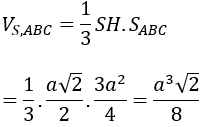
Bài 10: Cho khối chóp đều S.ABCD có cạnh đáy bằng a√3. Tính thể tích khối chóp S.ABCD biết mặt bên là tam giác đều.
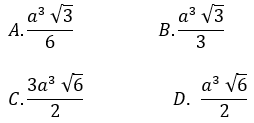
Lời giải:
Đáp án : D
Giải thích :
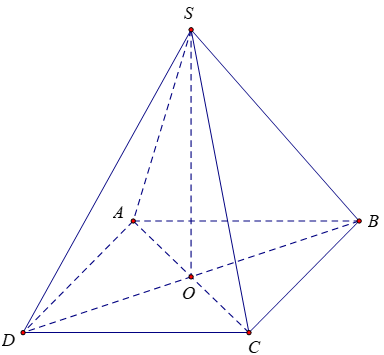
Gọi O là tâm của hình vuông ABCD khi đó SO ⊥ (ABCD)
∆SBC đều cạnh a√3 nên SC = a√3
Lại có: ABCD là hình vuông cạnh a√3, O là giao điểm của hai đường chéo