Cách giải bài tập về so sánh lũy thừa cực hay - Toán lớp 12

---

Cách giải bài tập về so sánh lũy thừa cực hay

Với Cách giải bài tập về so sánh lũy thừa cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về so sánh lũy thừa từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Để so sánh hai số ta sử dụng tính chất sau:

+ Tính chất 1

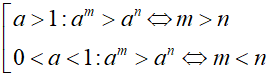
+ Tính chất 2. So sánh lũy thừa khác cơ số:

Với a > b > 0 thì

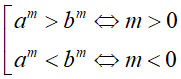
+ Chú ý:

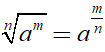
2. Ví dụ minh họa

Ví dụ 1. So sánh hai số m và n nếu (√13)^m > (√13)ⁿ

A. m > n    B. m = n

C. m < n    D. Không so sánh được.

Lời giải:

Đáp án: A

Do √13 > 1 nên (√13)^m > (√13)ⁿ ⇔ m > n .

Ví dụ 2. So sánh hai số m và n nếu

A. Không so sánh được. B. m = n

C. m > n D. m < n

Lời giải:

Đáp án: C

Do

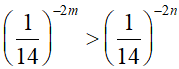
nên 14^2m > 14²ⁿ

Mà 14 > 1 nên 2m > 2n ⇔ m > n.

Ví dụ 3. Nếu (2√3 − 1)^{a + 2} < 2√3 − 1 thì

A. a < −1    B. a < 1    C. a > −1    D. a ≥ −1 .

Lời giải:

Đáp án: A

Do 2√3 − 1 > 1 nên (2√3 − 1)^{a + 2} < 2√3 − 1 ⇔ a + 2 < 1 ⇔ a < −1

Ví dụ 4. Nếu (√3 − √2)^{2m − 2} < √3 + √2 thì

Lời giải:

Đáp án: C

Ta có:

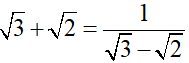
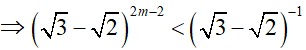
Mà 0 < √3 − √2 < 1 nên 2m − 2 > −1

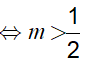
Ví dụ 5. Nếu 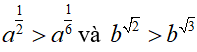thì

Lời giải:

Đáp án: D

+ Vì

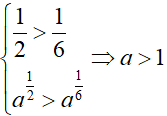
+ Và

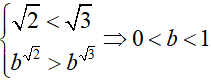
Ví dụ 6. Nếu (√ 3 − √2)^x > √3 + √2 thì

A. ∀x ∈ R .    B. x < 1    C. x > −1    D. x < −1

Lời giải:

Đáp án: D

+ Vì (√ 3 − √2).((√ 3 + √2)) = 1

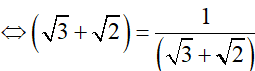
nên (√ 3 − √2)^x > √3 + √2

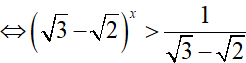
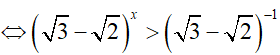
Mặt khác 0 < √3 − √2 < 1 => x < −1.

Ví dụ 7. Kết luận nào đúng về số thực a nếu

A. a > 2    B. a > 0    C. a > 1    D.1 < a < 2.

Lời giải:

Đáp án: A

Do

nên

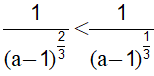
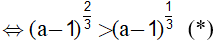
Mà

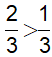
và số mũ không nguyên nên từ (*) suy ra:

a − 1 > 1 hay a > 2

Ví dụ 8. Kết luận nào đúng về số thực a nếu (3a + 9)⁻³ > (3a + 9)⁻²

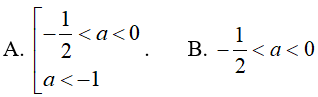
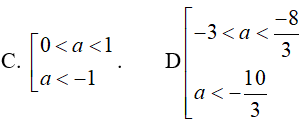
Lời giải:

Đáp án: D

Ta có: (3a + 9)⁻³ > (3a + 9)⁻²

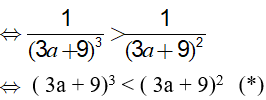
Do 3 > 2 và số mũ nguyên âm nên (*) xảy ra khi:

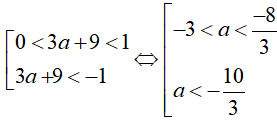
Ví dụ 9. Kết luận nào đúng về số thực a nếu

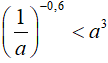
A. 0 < a < 1    B. a > 0    C. a > 1    D. a < 0

Lời giải:

Đáp án: C

Theo giả thiết ta có:

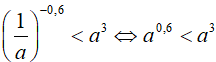
Do 0, 6 < 3 và có số mũ không nguyên nên a^0,6 < a³ khi a > 1.

Ví dụ 10. Kết luận nào đúng về số thực a nếu

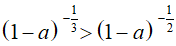
A. a < 0    B. a > 0    C.0 < a < 1    D. a > 1

Lời giải:

Đáp án: A

Ta có:

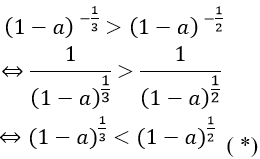
Do

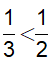
và số mũ không nguyên nên từ (*) suy ra 1 − a > 1 ⇔ a < 0 .

Ví dụ 11. Kết luận nào đúng về số thực a nếu

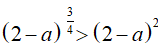
A. a > 1    B. 0 < a < 1.    C. 1 < a < 2 .    D. a < 1

Lời giải:

Đáp án: C

Do

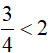
và có số mũ không nguyên nên

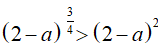
⇔ 0 < 2 − a < 1 ⇔ −2 < −a < −1 ⇔ 1 < a < 2

Ví dụ 12. Cho và Khẳng định nào sau đây là đúng

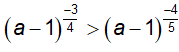
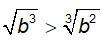
A. a; b > 1    B. 0 < a < 2; b > 1    C. 0 < a < 2; b < 1    D. a > 2; b > 1

Lời giải:

Đáp án: D

Ta có:

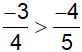
nên

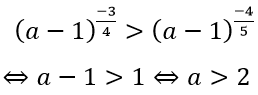
Mặt khác

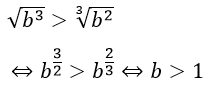
Do đó a > 2; b > 1

Ví dụ 13. Cho và Khẳng định nào sau đây là đúng

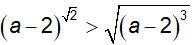
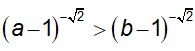
A. 2 < a < b    B. 2 < b < a < 3    C. b > a > 3    D. a > b > 3

Lời giải:

Đáp án: A

Ta có:

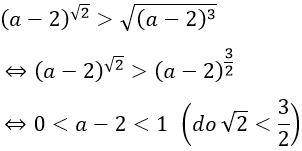
Suy ra: 2 < a < 3

Mặt khác

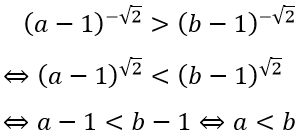
Trong các phương án chỉ có phương án A đúng.