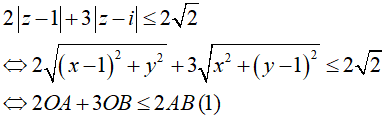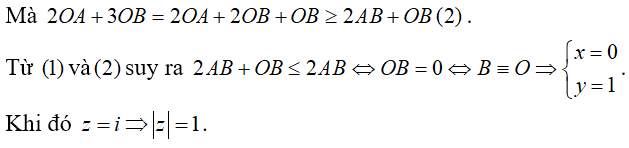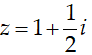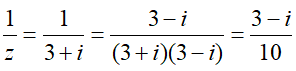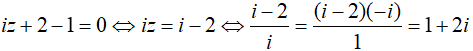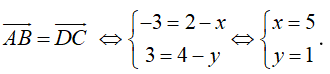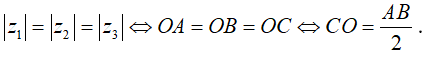Bài tập về Điểm biểu diễn số phức cực hay, chi tiết - Toán lớp 12
Bài tập về Điểm biểu diễn số phức cực hay, chi tiết
Với Bài tập về Điểm biểu diễn số phức cực hay, chi tiết Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về Điểm biểu diễn số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
A. Phương pháp giải & Ví dụ
1. Biểu diễn hình học số phức:
Khái niệm: Điểm M(a;b) biểu diễn cho số phức z = a + bi. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.
Chú ý: Để tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện nào đó ta gọi M(x;y) biểu diễn số phức z rồi dựa vào điều kiện đã cho để tìm một hệ thức liên hệ giữa x;y mà kết luận tập hợp điểm. Nếu
a) ax + by + c = 0 thì tập hợp điểm là đường thẳng
b) (x-a)2 + (y-b)2 = r2thì tập hợp điểm là đường tròn tâm I(a;b) bán kính r.
Dựa vào biểu diễn hình học của số phức: Điểm M(a;b) biểu diễn cho số phức z=a+bi. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.
Ví dụ minh họa
Ví dụ 1:Số phức z = 2 - 3i có điểm biểu diễn trên mặt phẳng tọa độ là:
A. M(2;3). B. M(-2;-3). C. M(2; -3). D. M(-2;3)
Hướng dẫn:
Chọn C.
Ví dụ 2:Cho số phức z = 2 - 3i. Điểm biểu diễn số phức liên hợp của z là
A.(2;3) . B. (-2;-3). C. (2;-3). D.(-2;3)
Hướng dẫn:
Vì z = 2 - 3i nên z = 2 + 3i.
Điểm biểu diễn của z có tọa độ (2;3).
Chọn A.
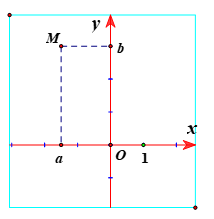
Ví dụ 3:Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm z?
A. z = -4 + 3i. B. z = 3 + 4i.
C. z = 3 - 4i. D. Z = -3 + 4i.
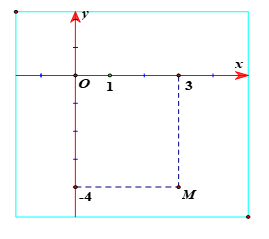
Hướng dẫn:
Ta có M(-3;4).
Vậy điểm M biểu diễn cho số phức z = 3 - 4i
Chọn C
Ví dụ 4:Cho số phức z có điểm biểu diễn là M. Biết rằng số phức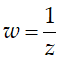 
được biểu diễn bởi điểm N gần với một trong bốn điểm , , , như hình vẽ bên.
Hỏi điểm N gần với điểm nào nhất?
A. S B.Q
C.P D.R
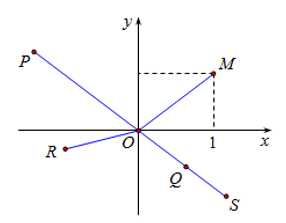
Hướng dẫn:
Cách 1: (Trắc nghiệm).
Ta có: z = a + bi theo hình vẽ có a = 1; 0 < b < 1 , a = 1, 0 < b < 1 nên ta chọn 
Suy ra: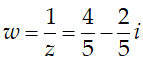 
và điểm cần tìm là Q.
Ta có: z = a + bi theo hình vẽ có a = 1 ; 0< b < 1
Ta có: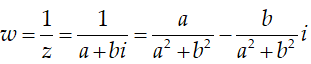 
có phần thực dương bé hơn 1 , phần ảo âm lớn hơn -1 nên ta chọn điểm Q là điểm cần tìm.
Chọn B.
Ví dụ 5:
a) Cho số phức z=6+8i. Số phức đối của z có tọa độ điểm biểu diễn là
A.(6; 8) B.(6;-8) C.(8; -6). D.(-6; -8)
b) Điểm M(2;-4) là điểm biểu diễn của số phức
A. z = 2 + 4i B. 2 - 4i C. z = -2i D. z = 4
Hướng dẫn:
a ) z = 6 + 8i nên số phức đối của z là w= -z = -6 - 8i
Vậy điểm biểu diễn của –z là (-6; -8)
Chọn đáp án D.
b) z = a + bi có điểm biểu diễn là M(a;b).
Ta suy ra z = 2 - 4i
Vậy chọn đáp án B.
B. Bài tập vận dụng
Câu 1:Cho số phức z = 3 + i. Điểm biểu diễn số phức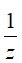 
trong mặt phẳng phức là:
Lời giải:
Đáp án : A
Giải thích :
Ta có : 
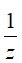
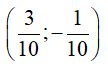
Do đó điểm biểu diễn số phức trong mặt phẳng phức là: 
Câu 2:Điểm M biểu diễn số phức z = 3 + 2i trong mặt phẳng tọa độ phức là:
A. M(3;2). B. M(2;3). C. M(3;-2). D.M(-3;-2).
Lời giải:
Đáp án : A
Câu 3:Cho số phức z = -2i - 1. Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2). B. M(-1;2). C. M(-2;1). D. M(2;-1).
Lời giải:
Đáp án : B
Giải thích :
Số phức liên hợp của z là z =-1+2i.
Do đó số phức liên hợp của z biểu diễn điểm M(-1;2) trên mặt phẳng tọa độ.
Câu 4:Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức w = 2 + 3i. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua trục tung.
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
Lời giải:
Đáp án : C
Giải thích :
Tọa độ điểm A và Bb lần lượt là: A(3;2) và B(2;3).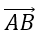
⃗=(-1;1 ).
Đường thẳng y = x hay x - y = 0 có vecto pháp tuyến là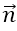 
⃗(1;-1).
Do 2 vecto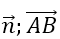 
⃗ là 2 vecto cùng phương nên đường thẳng AB vuông góc với đường thẳng y = x.
Gọi M(5/2; 5/2) là trung điểm AB; ta thấy M thuộc đường thẳng y = x. Do đó đường thẳng y = x là đường trung trực của AB.
Hay A và B đối xứng nhau qua y = x
Câu 5:Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A.2√5 B.√13 C.2√10 D.2√2
Lời giải:
Đáp án : C
Giải thích :
Ta có: 
Điểm biểu diễn của số phức z là A(1;2)
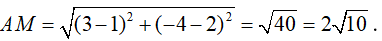
Câu 6:Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức Z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1 + 7i. B. 5 + i. C. 1 + 5i. D. 3 + 5i.
Lời giải:
Đáp án : B
Giải thích :
Ta có A(1 ;2) ; B(-2 ; 5),C(2 ;4).
Gọi D(x ; y).
Ta có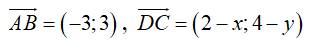 
Để ABCD là hình bình hành thì 
Vậy z = 5 + i.
Câu 7:Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z1 ; z2 ; z3. Biết |z1| = |z2| = |z3| và z1 + z2 = 0. Khi đó tam giác ABC là tam giác gì?
A. Tam giác ABC đều. B. Tam giác ABC vuông tại C.
C. Tam giác ABC cân tại C. D. Tam giác ABC vuông cân tại C
Lời giải:
Đáp án : B
Giải thích :
Vì z1 + z2 = 0 nên z1 ; z2 là hai số phức đối nhau, do đó hai điểm A: B đối xứng qua gốc O ( tức O là trung điểm của đoạn thẳng AB).
Lại có 
Vậy tam giác ABC có độ dài đường trung tuyến bằng một nửa cạnh huyền nên vuông tại C .
Câu 8:Xét số phức 2|z - 1| + 3|z - i| ≤ 2√2 thỏa mãn . Mệnh đề nào dưới đây đúng?
Lời giải:
Đáp án : D
Giải thích :
Giả sử z = x + yi có điểm biểu diễn là M(x;y).
Số phức z - 1có điểm biểu diễn A(x - 1; y) và z - 1 có điểm biểu diễn là B(x;y - 1).
Tacó
