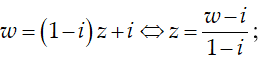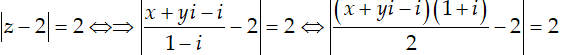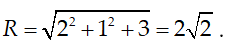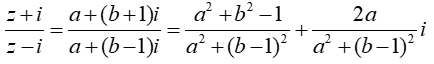Tập hợp điểm biểu diễn số phức là đường tròn cực hay - Toán lớp 12

Tập hợp điểm biểu diễn số phức là đường tròn cực hay

Với Tập hợp điểm biểu diễn số phức là đường tròn cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tập hợp điểm biểu diễn số phức là đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Ví dụ 1: Tập hợp các điểm M biểu diễn số phức |z -2 + 5i| = 4 thoả mãn là:

A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.

B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.

C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.

D. Đường tròn tâm O và bán kính bằng 2.

Hướng dẫn:

.Gọi số phức z = x + yi

|z -2 + 5i| = 4 <=> |x - 2 + (y + 5)i| = 4

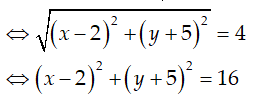
Vậy tập hợp điểm biểu diễn số phức là đường tròn tâm I(2; -5) bán kính R = 4.

Chọn C.

Ví dụ 2: Cho số phức z thỏa mãn |z - 2| = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = (1-i)z + i là một đường tròn. Tính bán kính r của đường tròn đó

A.2√2        B.r = 4        C.r = √2        D.r = 2

Hướng dẫn:

Ta có:

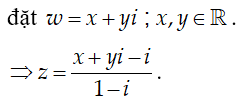
Ta có:

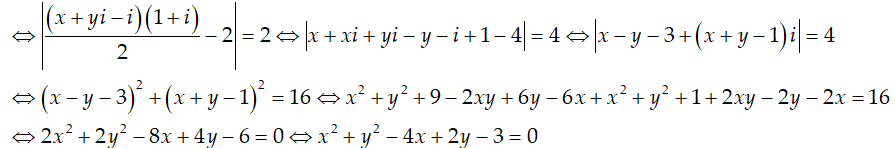
Đường tròn có bán kính là

Chọn A.

Ví dụ 3:Cho số phức z thỏa mãn |z -1| = 2 ; w = (1 + √3i)z + 2 .Tập hợp điểm biểu diễn của số phức w là đường tròn, tính bán kính đường tròn đó

A. R = 3        B. R = 2        C. R = 4        D. R = 5 .

Hướng dẫn:

w = (1 + √3i)z + 2 <=> w = (1 + √3i)(z -1) + 1 + √3i + 2

<=> w - (3 + √3i) = (1 + √3i)(z-1)

=> |w - (3 + √3i) | = | (1 + √3i)(z-1)| = |(1 + √3i)| |(z-1)| = 4

Chọn C.

Ví dụ 4:Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn 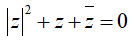là đường tròn C. Diện tích S của đường tròn C bằng bao nhiêu?

A.S = 4π        B.S = 2π        C.S = 3π        D.S = π

Hướng dẫn:

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi

Ta có:

|z|² + z + z = 0 <=> x² + y² + x + yi + x - yi = 0

<=>x² + y² + 2x = 0

=> bán kinh R = 1 => S = πR² = π

Chọn D

Ví dụ 5:xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z - 1 + 3i| ≤ 4 .

A. Hình tròn tâm I(-1;3), bán kính r = 4. B. Đường tròn tâm I(-1;3), bán kính r = 4.

C. Hình tròn tâm I(-1;-3), bán kính r = 4. D. Đường tròn tâm I(1;3), bán kính r = 4

Hướng dẫn:

Giả sử z = x + yi(x,y∈ R) , ta có z + 1 - 3i = x + 1 + (y-3)i.

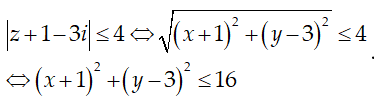
Vậy tập hợp các điểm trong mặt phẳng biểu diễn số phức z là hình tròn tâm I(-1; 3), bán kính r = 4.

Chọn A.

Ví dụ 6:Cho số phức z thỏa mãn 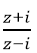là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:

A. Đường tròn tâm O, bán kính R = 1.

B. Hình tròn tâm O, bán kính R = 1 (kể cả biên).

C. Hình tròn tâm O, bán kính R = 1 (không kể biên).

D. Đường tròn tâm O, bán kính R = 1 bỏ đi một điểm (0;1)

Hướng dẫn:

Gọi M(a ; b) là điểm biểu diễn số phức z = a + bi

Ta có:

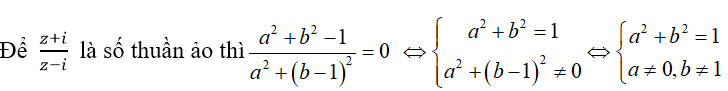
Tập hợp các điểm M là đường tròn tâm O, bán kính R=1 bỏ đi một điểm (0;1)

Đáp án D.

Ví dụ 7: Trong mặt phẳng phức Oxy, cho số phức z thỏa lần lượt một trong bốn điều kiện :

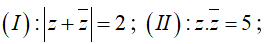
(III) : |z - 2i| = 4 , (IV) : |i(z - 4i)| = 3

Hỏi điều kiện nào để số phức z có tập hợp biểu diễn là đường thẳng.

Hướng dẫn:

A.(II),(III),(IV)        B.(I),(II)        C.(I)(IV)        D.(I)

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi

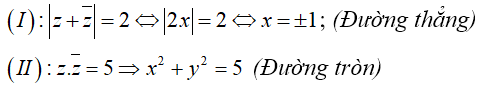
(III) : |z - 2i| = 4 <=> x² + (y-2)² = 16 ; (Đường tròn)

(IV) : |i(z - 4i)| = 3 <=> |4 + iz| = 3 <=> x² + (y - 4)² (Đường tròn)

Chọn D.

Ví dụ 8:Cho số phức z thỏa mãn điều kiện |z -3 + 4i| ≤ 2 . Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích

A. S = 9π        B.S = 12π        C.S = 16π        D.S = 25π

Hướng dẫn:

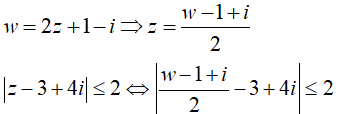
<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)

Giả sử w = x + yi , khi đó (1) <=> (x -7)² + (y + 9)² ≤ 16

Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4

Vậy diện tích cần tìm là S = π.4² = 16π

Chọn C.

Ví dụ 9:Trong mặt phẳng phức Oxy. tập hợp biểu diễn số phức z thỏa mãn 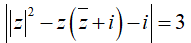là đường tròn C. Khoảng cách từ tâm I của đường tròn (C) đến trục tung bằng bao nhiêu?

A. d(I ; Oy) = 1.        B.d(I ; Oy) = 2.        C.d(I ; Oy) = 0.        D.d(I ; Oy) = √2 .

Hướng dẫn:

Gọi M(x ; y) là điểm biểu diễn số phức z = x + yi.

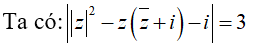
<=> |-iz - i| = 3 <=> |y + i(-x - 1)| = 3

<=> (x + 1)² + y ² = 9

Suy ra I(-1 ; 0) là tâm đường tròn (C)

=> d(I,Oy) = |X_I| = 1

Chọn đáp án A.