Tập hợp điểm biểu diễn số phức là một miền cực hay - Toán lớp 12

Tập hợp điểm biểu diễn số phức là một miền cực hay

Với Tập hợp điểm biểu diễn số phức là một miền cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tập hợp điểm biểu diễn số phức là một miền từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

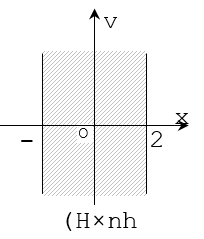
Ví dụ 1:Cho số phức z = a + bi. Để điểm biểu diễn của z nằm trong dải (- 2; 2), ở hình 1, điều kiện của a và b là:

A.a,b ∈ (-2,2) . B.a ∈ (-2,2) ; b ∈ R .

C.a ∈ R;b ∈ (-2,2) . D.a,b ∈ [-2,2] .

Hướng dẫn:

Các số phức trong dải đã cho có phần thực trong khoảng (-2;2), phần ảo tùy ý

Đáp án B.

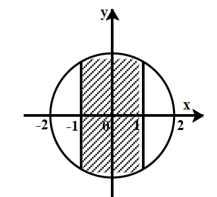
Ví dụ 2:Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo như trên hình.

A. Số phức z = a + bi ; |z| ≤ 2 ; a ∈ [-1;1] .

B. Số phức z = a + bi ; |z| ≤ 2 ; a ∉ [-1;1] .

C. Số phức z = a + bi ; |z| < 2 ; a ∈ [-1;1] .

D. Số phức z = a + bi ; |z| ≤ 2 ; b ∈ [-1;1] .

Hướng dẫn:

Từ hình biểu diễn ta thấy tập hợp các điểm M(a; b) biểu diễn số phức z trong phần gạch chéo đều thuộc đường tròn tâm O(0;0) và bán kính bằng 2; ngoài ra -1 ≤ a ≤ 1

Vậy M(a; b) là điểm biểu diễn của các số phức z = a + bi có mô đun nhỏ hơn hoặc bằng 2 và có phần thực thuộc đoạn [-1;1].

Chọn A.

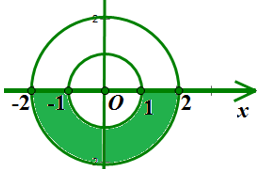
Ví dụ 3:Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ

A. 1 ≤ |z| ≤ 2 và phần ảo dương.

B. 1 ≤ |z| ≤ 2 và phần ảo âm.

C. 1 < |z| < 2 và phần ảo dương.

D. 1 < |z| < 2 và phần ảo âm.

Hướng dẫn:

Ta thấy phần tô màu là nửa dưới trục hoành của hình vành khăn được tạo bởi hai đường tròn đồng tâm O(0 ;0) và bán kính lần lượt là 1 và 2

Vậy đây chính là tập hợp các điểm M(x ;y) biểu diễn cho số phức z = x + yi trong mặt phẳng phức với 1 ≤ |z| ≤ 2 và có phần ảo âm.

Chọn B.