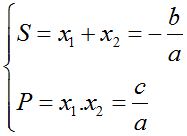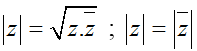Lý thuyết tổng hợp chương Số phức - Toán lớp 12

Lý thuyết tổng hợp chương Số phức

Tài liệu Lý thuyết tổng hợp chương Số phức Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về chương Số phức từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

** SỐ PHỨC VÀ CÁC PHÉP TOÁN

1. Phần thực và phần ảo của số phức, số phức liên hợp.

    a) Số phức z là biểu thức có dạng z = a + bi (a, b ∈ R, i² = -1) . Khi đó:

        + Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.

    b) Số phức liên hợp của z là .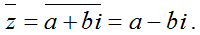

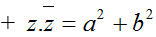
        + Tổng và tích của z và z− luôn là một số thực.

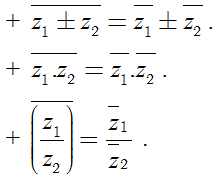
    Đặc biệt:

        + Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là z = a

        + Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (hay số thần ảo) và viết là

        + Số i = 0 + li = li.

        + Số: 0 = 0 + 0i vừa là số thực vừa là số ảo.

2. Số phức bằng nhau.

        + Cho hai số phức z₁ = a₁ + b₁i, z₂ + b₂i (a₁, a₂, b₁, b₂ ∈ R). Khi đó:

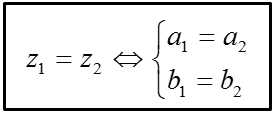
3. Biểu diễn hình học của số phức, mô đun của số phức.

    a) Biễu diễn hình học của số phức.

    + Số phức z = a + bi (a, b ∈ R) được biểu diễn bởi điểm M(a; b) trong mặt phẳng tọa độ.

    + z và z− được biểu diễn bởi hai điểm đối xứng nhau qua trục 0x.

    b) Mô đun của số phức.

    + Mô đun của số phức z là .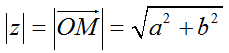

    +

4. Cộng, trừ, nhân, chia số phức.

    Cho hai số phức z₁ = a + bi và z₂ = c + di thì:

    • Phép cộng số phức: z₁ + z₂ = (a + c) + (b + d)i

    • Phép trừ số phức: z₁ - z₂ = (a - c) + (b - d)i

    • Phép nhân số phức: z₁.z₂ = (ac - bd) + (ad + bc)i

    • Phép chia số phức: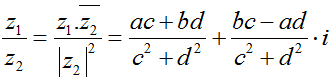 (với z₂ ≠ 0)

** PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC

    Cho phương trình bậc hai ax² + bx + c = 0 (a, b, c ∈ R; a ≠ 0). Xét Δ = b² - 4ac, ta có

    • Δ = 0: phương trình có nghiệm thực x = -b/2a .

    • Δ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức: .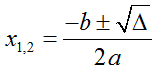

    • Δ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức: .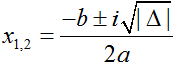

    ** Chú ý.

    - Mọi phương trình bậc n: A₀zⁿ + A₁z^n-1 + ... + A_n-1z + A_n = 0 luôn có n nghiệm phức (không nhất thiết phân biệt).

    - Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x₁, x₂ (thực hoặc phức). Ta có hệ thức Vi–ét