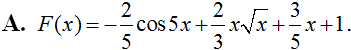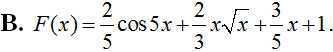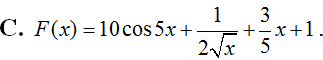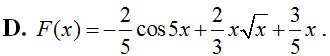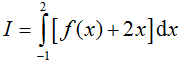Một nguyên hàm F(x) của hàm số f(x)=2sin5x+x+3/5 thỏa mãn đồ thị của hai hàm số F(x) và
Câu hỏi:
Một nguyên hàm F(x) của hàm số thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:
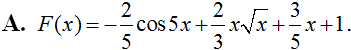
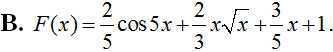
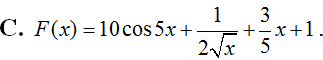
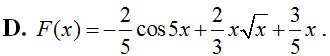
Trả lời:
Chọn A.
Ta có F(x)=-
và F(0) = f(0) ⇔ C = 1
Vậy F(x)= -
Xem thêm bài tập Toán có lời giải hay khác:
Câu 5:
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 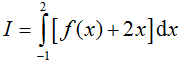 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
Xem lời giải »
Câu 6:
Cho Tính
Xem lời giải »
Câu 7:
Cho hàm số f(x) liên tục trên đoạn [0; 10] thỏa mãn . Tính .
Xem lời giải »
Câu 8:
Hàm số là một nguyên hàm cùa hàm số thì a + b + c bằng:
Xem lời giải »