Nếu log83 = p và log35 = q thì log 5 bằng
Câu hỏi:
Nếu log83 = p và log35 = q thì log 5 bằng:
A.
B.
C. p.q
D.
Trả lời:
Chọn B.
Ta có: 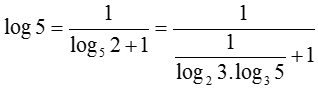
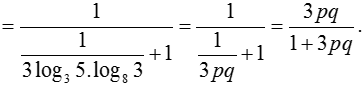
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho x > 0 và y > 0. Viết biểu thức ; về dạng và biểu thức về dạng . Ta có m – n = ?
Xem lời giải »
Câu 2:
Viết biểu thức về dạng và biểu thức về dạng 2y. Ta có x + y bằng
Xem lời giải »
Câu 5:
Biết log275 = a; log87 = b; log23 = c thì log12 35 tính theo a; b; c bằng:
Xem lời giải »
Câu 6:
Cho log23 = a; log35 = b; log72 = c . Hãy tính log14063 theo a; b; c
Xem lời giải »
Câu 7:
Cho logba = x và logbc = y . Hãy biểu diễn theo x và y:
Xem lời giải »
Câu 8:
Cho , với a> 1 ; b> 1 và . Tìm m sao cho P đạt giá trị nhỏ nhất.
Xem lời giải »
