Phương trình 2^log5(x+3) = x có tất cả bao nhiêu nghiệm

❮ Bài trước Bài sau ❯

Câu hỏi:

Phương trình $2^{\log_{5} (x + 3)} = x$ có tất cả bao nhiêu nghiệm?

A. 1.

B. 2.

C. 3.

D. 0.

Trả lời:

Chọn A.

Điều kiện: x> 0.

Lấy logarit cơ số của hai vế phương trình, ta được log₅(x+3)= log₂x

Do 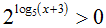nên để phương trình có nghiệm thì x > 2

Lấy logarit cơ số của hai vế phương trình, ta được log₅(x + 3) = log₂x.

Đặt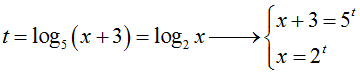

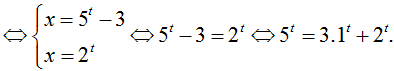
Chia hai vế phương trình cho 5^t, ta được 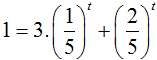. Đây là phương trình hoành độ giao điểm của đường thẳng y = 1 (hàm hằng) và đồ thị hàm số 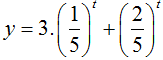(hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến).

Do đó phương trình có nghiệm duy nhất. Nhận thấy t = 1 thỏa mãn phương trình. Với t = 1 thì x = 2 (thỏa mãn).

Vậy phương trình có nghiệm duy nhất.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Xét các số thực dương thỏa mãn $\log_{3} \frac{1 - x y}{x + 2 y} = 3 x y + x + 2 y - 4$ . Tìm giá trị nhỏ nhất S_min của S = x + y

Xem lời giải »

Câu 2:

Cho hai số thực dương a; b thỏa mãn log₂(a + 1) + log₂(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là

Xem lời giải »

Câu 3:

Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất P_min của biểu thức $P = \log_{\frac{a}{b}}^{2} (a^{2}) + 3 \log_{b} \frac{a}{b}$

Xem lời giải »

Câu 4:

Số nghiệm của phương trình: $9^{x + \log_{3} 2} - 2 = 3^{x + \log_{3} 2}$ là

Xem lời giải »

Câu 5:

Gọi T là tổng tất cả các nghiệm của phương trình $3^{x^{2}} . 2^{x} = 1$ . Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 6:

Cho hàm số $f (x) = 3^{x + 1} . 5^{x^{2}}$ . Mệnh đề nào sau đây là sai?

Xem lời giải »

Câu 7:

Gọi x₀ là nghiệm nguyên của phương trình $5^{x} . 8^{\frac{x}{x + 1}} = 100$ . Tính giá trị của biểu thức P = x₀(5 - x₀)( x₀+ 8).

Xem lời giải »

Câu 8:

Phương trình $3^{x^{2} - 2} . 4^{\frac{2 x - 3}{x}} = 18$ có tất cả bao nhiêu nghiệm?

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Phương trình 2^log5(x+3) = x có tất cả bao nhiêu nghiệm

Xem thêm bài tập Toán có lời giải hay khác: